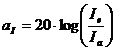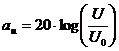Kondensator und Spule
im Wechselstromkreis
Kondensator im
Wechselstromkreis
Der ideale Kondensator
Spannung und Strom
Für den Betrag des Stromes im Kondensator gilt:
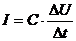
Hieraus folgt, dass nur bei einer Anderung der Spannung am Kondensator
eine Stromänderung eintritt. Daraus folgert sich, dass bei sinusförmiger
Wechselspannung, im Gegensatz zu Gleichspannung, dauernd ein Strom durch den
Kondensator fliessen muss. Dabei hat der Strom einen mathematischen ähnlichen
Verlauf wie die Spannung. Er eilt der Spannung um 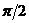 vor.
vor.
Um die zeitlich nicht konstanten Werte der Spannung und des Stromes zu
berechnen verwenden wir die Formel für die allgemeine Sinusfunktion:
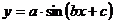
Dabei entspricht y dem Momentanwert, a dem Maximalwert, b der
Kreisfrequenz (in unserem Fall  ) und c der Phasenverschiebung. Als unabhängige Variable x
verwenden wir die Zeit t.
) und c der Phasenverschiebung. Als unabhängige Variable x
verwenden wir die Zeit t.
Widerstand
Der Widerstand, der der Kondensator dem Strom entgegensetzt, ist
frequenzabhängig. Wir sprechen daher nicht von einem Widerstand im
herkömmlichen Sinn (Wirkwiderstand), sondern nennen ihn Blindwiderstand. Er
berechnet sich:

Je grösser die Kapazität und je höher die Frequenz, desto tiefer der
kapazitive Blindwiderstand. Im Widerstands-Frequenz-Diagramm bildet sich eine
Hyperbel. Sie ist um so ausgeprägter, je grösser die Kapazität ist.
Leistung
Wird nach der Formel 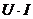 die Leistung für jeden
Zeitpunkt während einer Periode berechnet, so erhalten wir eine Kurve, deren
arithmetischer Mittelwert gleich Null ist. Der ideale Kondensator gibt demnach
jeweils die gleiche Leistung ab, wie er aufnimmt (Wirkleistung ist Null). Die
innerhalb des Kondensators umgesetzte Leistung nennt man Blindleistung. Sie
berechnet sich:
die Leistung für jeden
Zeitpunkt während einer Periode berechnet, so erhalten wir eine Kurve, deren
arithmetischer Mittelwert gleich Null ist. Der ideale Kondensator gibt demnach
jeweils die gleiche Leistung ab, wie er aufnimmt (Wirkleistung ist Null). Die
innerhalb des Kondensators umgesetzte Leistung nennt man Blindleistung. Sie
berechnet sich:
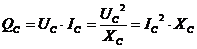
Ihre Einheit ist [var].
Der reale Kondensator
Bedingt durch ein nicht ideales Dielektrikum, Erwärmungs- und
Umpolungsverluste (elektrisches Wechselfeld) lässt sich ein realer Kondensator
durch eine Parallelschaltung aus einem idealem Kondensator und einem Widerstand
darstellen.
Die Spannung ist an beiden Komponenten dieselbe, während wir den
Gesamtstrom aus der geometrischen Addition der Teilströme errechnen. Das
gleiche Verfahren wenden wir an, um die Leitwerte (Parallelschaltung) und
Leistungen zu ermitteln.
Die Güte Q
Die Güte Q ist das Verhältnis der Blindgrösse zur Wirkgrösse. Je
kleiner die Wirkgrösse, desto grösser die Güte und desto "besser" der
Kondensator. Da die Güte das Verhältnis der Katheten am Vektordreieck bestimmt,
bestimmt sie auch dessen Winkel und damit die Phasenwinkel zwischen Schein-,
Wirk- und Blindgrösse.
Der Verlustfaktor d
Der Verlustfaktor d ist des Verhältnis der Wirkgrösse zur Blindgrösse.
Je grösser die Wirkgrösse, desto grösser der Verlustfaktor und desto
"schlechter" der Kondensator. Der Verlustfaktor d ist die inverse Grösse zur
Güte Q.
Spule im
Wechselstromkreis
Die ideale Spule
Spannung und Strom
Für den Betrag der Spannung in der Spule gilt:

Hieraus folgt, dass nur bei einer Anderung des Stromes in der Spule
eine Spannungsänderung eintritt. Dabei hat die Spannung einen mathematisch
ähnlichen Verlauf wie der Strom. Sie eilt dem Strom um 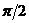 vor.
vor.
Um die zeitlich nicht konstanten Werte der Spannung und des Stromes zu
berechnen verwenden wir die Formel für die allgemeine Sinusfunktion:
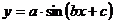
Dabei entspricht y dem Momentanwert, a dem Maximalwert, b der
Kreisfrequenz (in unserem Fall  ) und c der Phasenverschiebung. Als unabhängige Variable x
verwenden wir die Zeit t.
) und c der Phasenverschiebung. Als unabhängige Variable x
verwenden wir die Zeit t.
Widerstand
Der Widerstand, der die Spule dem Strom entgegensetzt, ist
frequenzabhängig. Wir sprechen daher nicht von einem Widerstand im
herkömmlichen Sinn (Wirkwiderstand), sondern nennen ihn Blindwiderstand. Er
berechnet sich:
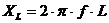
Je grösser die Induktivität und je höher die Frequenz, desto grösser
der induktive Blindwiderstand. Im Widerstands-Frequenz-Diagramm bildet sich
eine Gerade. Sie ist um so steiler, je grösser die Induktivität ist.
Leistung
Wird nach der Formel 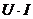 die Leistung für jeden
Zeitpunkt während einer Periode berechnet, so erhalten wir eine Kurve, deren
arithmetischer Mittelwert gleich Null ist. Die ideale Spule gibt demnach
jeweils die gleiche Leistung ab, wie sie aufnimmt (Wirkleistung ist Null). Die
innerhalb der Spule umgesetzte Leistung nennt man Blindleistung. Sie berechnet
sich:
die Leistung für jeden
Zeitpunkt während einer Periode berechnet, so erhalten wir eine Kurve, deren
arithmetischer Mittelwert gleich Null ist. Die ideale Spule gibt demnach
jeweils die gleiche Leistung ab, wie sie aufnimmt (Wirkleistung ist Null). Die
innerhalb der Spule umgesetzte Leistung nennt man Blindleistung. Sie berechnet
sich:
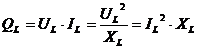
Ihre Einheit ist [var].
Die reale Spule
Bedingt durch Wicklungs-, Wirbelstrom- und Hystereseverluste lässt sich
eine reale Spule durch eine Serieschaltung aus idealer Spule und einem
Widerstand darstellen.
Der Strom ist in beiden Komponenten der selbe, während wir die
Gesamtspannung aus der geometrischen Addition der Teilspannungen errechnen. Das
gleiche Verfahren wenden wir an, um die Widerstände und Leistungen zu
ermitteln.
Die Güte Q
Die Güte Q ist das Verhältnis der Blindgrösse zur Wirkgrösse. Je
kleiner die Wirkgrösse, desto grösser die Güte und desto "besser" der
Kondensator. Da die Güte das Verhältnis der Katheten am Vektordreieck bestimmt,
bestimmt sie auch dessen Winkel und damit die Phasenwinkel zwischen Schein-,
Wirk- und Blindgrösse.
Der Verlustfaktor d
Der Verlustfaktor d ist des Verhältnis der Wirkgrösse zur Blindgrösse.
Je grösser die Wirkgrösse, desto grösser der Verlustfaktor und desto
"schlechter" der Kondensator. Der Verlustfaktor d ist die inverse Grösse zur
Güte Q.
Kompensation
Serieschaltung
In einer Serieschaltung eines Widerstandes, einer Spule und eines
Kondensators gilt:
UL
eilt UR um 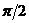 vor oder UC
eilt UR um
vor oder UC
eilt UR um 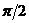 nach, da der Strom in
allen Elementen gleich gross ist.
nach, da der Strom in
allen Elementen gleich gross ist.
Daraus folgt, dass UC und UL um  verschoben sind und
daher genau entgegengesetzt liegen. Durch Anfügen einer Induktivität an ein
RC-Glied lässt sich somit die Wirkung des Kondensators kompensieren (ein
Kondensator kompensiert die Induktivität eines RL-Glieds).
verschoben sind und
daher genau entgegengesetzt liegen. Durch Anfügen einer Induktivität an ein
RC-Glied lässt sich somit die Wirkung des Kondensators kompensieren (ein
Kondensator kompensiert die Induktivität eines RL-Glieds).
Zur Berechnung der Scheingrössen von Spannungen, Widerständen und
Leistungen müssen wir folglich die Wirkgrösse geometrisch zur Differenz der
Blindgrössen addieren.
Die betragsmässig grössere Komponente der Blindgrössen bestimmt das
Verhalten der Schaltung.
Parallelschaltung
In einer Parallelschaltung eines Widerstandes, einer Spule und eines
Kondensators gilt:
IL
eilt IR um 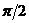 nach oder IC
eilt IR um
nach oder IC
eilt IR um 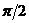 vor, da die Spannung
an allen Elementen gleich gross ist.
vor, da die Spannung
an allen Elementen gleich gross ist.
Daraus folgt, dass IC und IL um  verschoben sind und
daher genau entgegengesetzt liegen. Durch Anfügen einer Induktivität an ein
RC-Glied lässt sich somit die Wirkung des Kondensators kompensieren (ein
Kondensator kompensiert die Induktivität eines RL-Glieds).
verschoben sind und
daher genau entgegengesetzt liegen. Durch Anfügen einer Induktivität an ein
RC-Glied lässt sich somit die Wirkung des Kondensators kompensieren (ein
Kondensator kompensiert die Induktivität eines RL-Glieds).
Zur Berechnung der Scheingrössen von Strömen, Leitwerten und Leistungen
müssen wir folglich die Wirkgrösse geometrisch zur Differenz der Blindgrössen
addieren.
Die betragsmässig grössere Komponente der Blindgrössen bestimmt das
Verhalten der Schaltung.
Impulsverformung
RC-Integrierglied
In einem RC-Glied an Gleichspannung lädt sich der Kondensator nach
einer Exponentialfunktion auf. Falls die Eingangsspannung wegfällt, entlädt
sich der Kondensator wiederum nach einer Exponentialfunktion. Je nach Wahl der
Zeitkonstante werden die Spannungszu- und abnahmen annähernd linear. Wird die
Zeitkonstante grösser als eine Periodendauer des Eingangssignals, so entsteht
eine Gleichspannung mit halber Höhe der Eingangsimpulse, da Anderungen des
Eingangs kaum noch Auswirkungen auf die Ladung des Kondensators haben. Es lässt
sich also sagen, dass der Spannungsverlauf am Kondensator die "Fläche unter der
Kurve des Eingangssignals" darstellt. Er integriert (Integration = Erhöhung des
Grades einer Funktion) demnach das Eingangssignal.
Allgemein wählt man:

CR-Differenzierglied
In einem CR-Differenzierglied an Gleichspannung fällt die gesamte
Spannung am Kondensator ab. Am Ausgang (Widerstand) fällt folglich keine
Spannung ab. Nur bei einer Spannungsänderung am Eingang des Glieds kann ein
Strom den Kondensator passieren und am Widerstand einen Spannungsabfall erzeugen.
Das Glied differenziert (Differentation = Reduktion des Grades einer Funktion)
demnach das Eingangssignal. Wird die Zeitkonstante grösser als eine
Periodendauer des Eingangssignals, so kann sich der Kondensator nicht mehr
entladen und wir erhalten wiederum das Eingangssignal, jedoch ohne DC-Anteil.
Allgemein wählt man:

Siebschaltungen
Tiefpass
Als passive Tiefpässe kommen entweder RC-Glieder oder LR-Glieder in
Frage. Im ersten Fall werden Spannungen mit hohen Frequenzen am Ausgang durch
den Kondensator kurzgeschlossen und nur Spannungen mit tiefen Frequenzen am
Ausgang zur Verfügung gestellt. Im zweiten Fall erhöhen hochfrequente Signale
den Widerstand der Spule und am Ausgangswiderstand fällt keine Spannung mehr
ab. Bei niederfrequenten Signalen fällt der Widerstand der Spule kaum mehr ins
Gewicht und sie stehen am Ausgangswiderstand zur Verfügung.
Mit sich ändernder Frequenz ändern sich auch laufend die Verhältnisse
der Katheten am Vektordreieck und damit die Winkel, u.a. der Winkel zwischen
der Schein- und der Wirkgrösse. Dieser Winkel stellt den Phasenwinkel dar. Er
läuft mit zunehmender Frequenz von 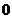 gegen
gegen 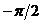 .
.
Grenzfrequenz
Sie ist definiert als die Frequenz, wo die Wirkgrösse gleich der
Blindgrösse ist:

Daraus folgt die Grösse des Phasenwinkels bei Grenzfrequenz:
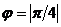
Die Grenzfrequenz berechnet sich wie folgt:
RC: 
LR: 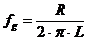
Die Grenzfrequenz ist ebenfalls die Frequenz, bei das Ausgangssignal um
-3dB gegenüber des Höchstwertes abgesunken ist:
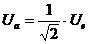
Hochpass
Als passive Hochpässe kommen entweder CR-Glieder oder RL-Glieder in
Frage. Im ersten Fall fallen niederfrequente Signale am Kondensator ab. Nur
hochfrequente Signale passieren den Kondensator und stehen am
Ausgangswiderstand zur Verfügung. Im zweiten Fall werden niederfrequente
Signale durch die Spule am Ausgang kurzgeschlossen und nur hochfrequente
Signale können an der Spule abfallen.
Mit sich ändernder Frequenz ändern sich auch laufend die Verhältnisse
der Katheten am Vektordreieck und damit die Winkel, u.a. der Winkel zwischen
der Schein- und der Wirkgrösse. Dieser Winkel stellt den Phasenwinkel dar. Er
läuft mit zunehmender Frequenz von  gegen
gegen 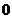 .
.
Bandpass
Als passive Bandpässe kommen LC- oder RC-Bandpässe in Frage. Sie lassen
nur Signale in einem bestimmten Frequenzbereich passieren.
Bandsperre
Als passive Bandsperren kommen LC-Bandsperren oder Wien-Robinson-Brücken
in Frage. Sie unterdrücken Signale in einem bestimmten Frequenzbereich.
Schwingkreise
Serieschwingkreis
Ein Serieschwingkreis besteht aus einer Kapazität, einer Induktivität
und einem ohmschen Widerstand. Bei einer ganz bestimmten Frequenz wird der
kapazitive Blindwiderstand gleich dem induktiven Blindwiderstand (Wir rechnen
mit dem Widerstand, da er proportional zur Spannung ist; der Strom ist in allen
Elementen gleich gross). Da sie entgegengesetzt gerichtet sind, heben sie sich
gegenseitig auf. Die Impedanz des Schwingkreises wird gleich dem ohmschen
Widerstand (reiner Wirkwiderstand). Übers ganze Glied gesehen besteht keine
Phasenverschiebung mehr.
Der Serieschwingkreis ist daher eine Filterschaltung, welche nur
Frequenzen in einem ganz bestimmten Frequenzbereich passieren lässt (auch
Saugkreis genannt).
Resonanzfrequenz
Die Frequenz, bei der dieser Fall eintritt, heisst Resonanzfrequenz.
Sie berechnet sich:
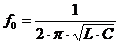
Diese Formel ist auch unter dem Begriff Thomson'sche Schwingungsformel
bekannt.
Je nach Dimensionierung des Kreises, können an den Blindelementen
Spannungen abfallen, die weitaus höher als die am Eingang des Kreises angelegte
Spannung sind (Spannungsüberhöhung).
Güte Q
Das Verhältnis der Katheten am Vektordreieck (Blindgrösse zu
Wirkgrösse) nennt man die Güte Q eines Kreises. Sie gibt an, wie viel mal
grösser die Spannung bei Resonanz an der Induktivität und dem Kondensator ist.
Dämpfung d
Die Dämpfung d ist die inverse Grösse zur Güte Q. Sie drückt das
Verhältnis von Wirkgrösse zur Blindgrösse aus.
Bandbreite b
Sie gibt die Breite des Frequenzbandes zwischen der unteren und der
oberen Grenzfrequenz an.

Aus den Formeln für die Güte erhalten wir:
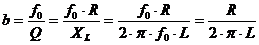
Einfluss der ohmschen
Grösse auf die Güte und die Bandbreite
Wird ein grosser ohmscher Widerstand gewählt, ist die Güte des Kreises
klein, während dafür die Bandbreite gross ist. Wird dagegen der ohmsche
Widerstand verkleinert, nimmt die Güte zu; die Bandbreite wird jedoch kleiner.
Parallelschwingkreis
Ein Parallelschwingkreis besteht aus einer Kapazität, einer
Induktivität und einem ohmschen Widerstand. Bei einer ganz bestimmten Frequenz
wird der kapazitive Blindleitwert gleich dem induktiven Blindleitwert (Wir
rechnen mit dem Leitwert, da er proportional zum Strom ist; die Spannung ist an
allen Elementen gleich gross). Da sie entgegengesetzt gerichtet sind, heben sie
sich gegenseitig auf. Die Admitanz des Schwingkreises wird gleich dem ohmschen
Leitwert (reiner Wirkleitwert). Übers ganze Glied gesehen besteht keine
Phasenverschiebung mehr.
Der Parallelschwingkreis ist daher eine Filterschaltung, welche
Frequenzen in einem ganz bestimmten Frequenzbereich herausfiltert (auch Sperrkreis
genannt).
Zur Berechnung der Resonanzfrequenz gilt die Thomson'sche
Schwingungsformel.
Je nach Dimensionierung des Kreises, können an den Blindelementen
Ströme auftreten, die weitaus höher als die am Eingang des Kreises fliessenden
Ströme sind (Stromüberhöhung).
Verluste
Ein idealer Parallelschwingkreis bestünde nur aus einer Kapazität und
einer Induktivität. In der Spule treten aber ohmsche Verluste auf. Diese sind
in Serie zur Spule. Um das gewohnte Bild eines Parallelschwingkreises zu
erhalten, rechnen wir den Seriewiderstand in einen Parallelwiderstand um. Für
den Resonanzfall lässt er sich nach folgender Formel berechnen:

Verstärkung und
Dämpfung
Verstärkungs- und
Dämpfungsfaktor
Elektrische Schaltungen können allgemein als Vierpol dargestellt
werden. Aus den Verhältnissen von Ausgangsgrösse zu Eingangsgrösse erhalten wir
die Verstärkungsfaktoren V. Aus den Verhältnissen von Eingangsgrösse zu
Ausgangsgrösse erhalten wir die Dämpfungsfaktoren D.
Beispiel Leistungsverstärkungsfaktor:
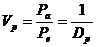
Beziehung zwischen
Verstärkungs- und Dämpfungsfaktor
Es gilt der Zusammenhang:
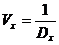
Verstärkungs- und
Dämpfungsmass
Eine alternative
Darstellungsform bietet die Umrechnung der Faktoren in Masse. Das Mass ist der
Logarithmus mit der Basis 10 des Faktors. Um jedoch etwas grössere Zahlen zu
erhalten, multiplizieren wir noch mit dem Wert 20 (beim
Leistungsverstärkungsmass nur mit 10). Die Einheit des Masses ist Dezibel. Als
Formelzeichen verwenden wir die Kleinbuchstaben v und a.
Beispiel Stromdämpfungsmass:
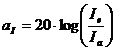
Beziehung zwischen
Verstärkungs- und Dämpfungsmass
Es gilt der Zusammenhang:

Absoluter Pegel
Für die Hochfrequenz- und
die Fernmeldetechnik wurde eine feste Bezugsgrösse definiert:
Hochfrequenztechnik: U0=1E-6V
Fernmeldetechnik: U0=0,775V
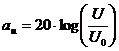
Dämpfungsbelag
Der Dämpfungsbelag gibt an,
wie gross die Dämpfung in jeder Streckeneinheit ist:
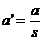
Als Einheit drängt sich
[dB/m] auf.