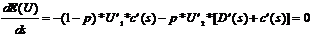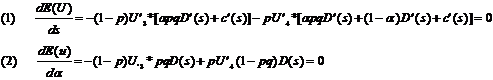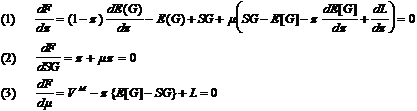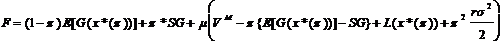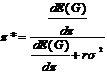 |
|
|
|
Ähnliche Berichte:
|
Papers in anderen sprachen:
|
|
geographie referate |
Kolloquium Neue Institutionenökonomik
Hausarbeit:
Moral Hazard
und
Incentives
Inhaltsverzeichnis
I. Einleitung
II. Grundlagen
A. Heterogene Güter und Transaktionskosten
B. Informationsasymmetrie
C. Principal-Agent-Modelle
1. Zwei Parteien
2. Hidden action
3. Hidden information
III. Moral Hazard
A. Einführung
1. Was ist moral hazard?
2. Beispiele für Moral hazard
B. Mikrotheoretische Überlegungen
1. Der Modellrahmen
2. Ohne Versicherungsmöglichkeit
3. Mit Versicherungsmöglichkeit
4. Vergleich der optimalen Schadensverhütung mit und ohne Versicherung
C. Der Unterschied zwischen moral hazard und adverse selection
1. Was ist adverse selection?
2. Unterschiede beim Selektionsmechanismus
IV. Incentives
A. Einführung
1. Warum braucht man incentives?
2. Beispiele für incentives
B. Mikrotheoretische Überlegungen bei Risikoneutralität
1. Der Modellrahmen
2. Das Kalkül des Agenten
3. Die optimale Prämienfunktion
4. Graphische Interpretation
C. Mikrotheoretische Überlegungen bei Risikoaversion
1. Erweiterung des Modellrahmens
2. Das Kalkül des Agenten
3. Die optimale Prämienfunktion
4. Graphische Interpretation
V. Schlußbemerkungen
VI. Anhang
A. Wie sieht die optimale Bezahlung eines Handelsvertreters aus?
1. Aktionen und Ergebnisse
2. Der Nutzen des Agenten
3. Das Kalkül des Unternehmens
4. Der Vertrag zwischen Unternehmung und Vertreter
5. Interpretation
B. Tabellarische Zusammenfassung des Beispiels
VII. Literaturverzeichnis
Symbolverzeichnis
a - Deckungsgrad der Versicherung
p - Prämiensatz des Agenten
(1-a) - Selbstbeteiligung des Versicherten
(1-p) - Wahrscheinlichkeit, daß kein Schaden auftritt
s - Varianz des Erfolges
c(s) - Kosten der Schadensverhütung
D(s) - Höhe des Schadens, abhängig von s
E(G) - erwarteter Gewinn
E(P) - erwartete Prämie
E(U) - erwarteter Nutzen
G - Erfolg des Agenten
L(x) - Arbeitsleid des Agenten, abhängig von seinem Leistungsniveau
p - Wahrscheinlichkeit, daß ein Schaden auftritt;
P(G) - Prämienfunktion (abhängig vom Erfolg des Agenten)
q - Zuschlag der Versicherung auf den erwarteten Schaden, um Betriebskosten zu decken
r - Grad der Risikoaversion des Agenten
s - Maß für das Schadensverhütungsniveau
SA(P) - Sicherheitsäquivalent des Agenten
SG - Soll-Erfolg des Agenten
VM - Mindestnutzen des Agenten
w - Vermögen des Wirtschaftssubjektes zu Beginn der Periode
x(p) - Reaktionsfunktion des Agenten (in Abhängigkeit vom Prämiensatz)
Die Vertreter der "Neue Institutionenökonomik" versuchen, durch eine Erweiterung der klassischen Annahmen die Wirkung und den Wandel von Institutionen zu erklären. Eine Institution muß nicht unbedingt eine Behörde oder ein Amt sein, unter Institution wird ganz allgemein " die vertragliche Regelung einer Kooperation im weitesten Sinne zwischen zwei Personen(gruppen)" verstanden, also etwa zwischen einer Versicherung und einem Versicherungsnehmer oder ein Arbeitsvertrag.
In der vorliegenden Arbeit geht es darum, bestimmte Konsequenzen zu analysieren, die sich aus vertraglichen Beziehungen ergeben können und darum, wie eine effiziente Steuerung des Verhaltens der Wirtschaftssubjekte erreicht werden kann. Dabei werden der Markt für Versicherungen und Probleme von Arbeitsverträgen betrachtet, da für beide Fälle die Probleme sehr deutlich sichtbar werden.
Zunächst möchte ich einige grundlegende Dinge abhandeln, die Voraussetzung sind für das Auftreten von moral hazard. Ganz grundsätzlich wird dann geprüft, warum sich moral hazard für ein rationales Wirtschaftssubjekt lohnt. Da moral hazard häufig mit Versicherungen in Verbindung gebracht wird, ist diese Darstellung ist am Versicherungsmarkt orientiert.
Anreizsysteme können bei Arbeitsverträgen einfach nachvollziehbar gezeigt werden. Deshalb behandelt der Abschnitt incentives die Bezahlung eines Angestellten. Da der Grad der Risikoaversion der handelnden Wirtschaftssubjekte bei Anreizen eine zentrale Rolle spielt, untersuche ich erst Anreizstrukturen für risikoneutrale, dann für risikoaverse Agenten. Risikoaversion des Prinzipals wird nicht behandelt.
Im Anhang beschreibe ich ein Beispiel für ein Anreizsystem. Hier wird an einem praktischen Fall gezeigt, wie incentives aussehen können. Aufbauend auf der formalen Betrachtung der Anreizsysteme im Unternehmenssektor wird die Beziehung zwischen einem Unternehmen und seinem Handelsvertreter untersucht.
Die Annahme des "homogenen Gutes" in der klassischen Mikroökonomik ist sehr restriktiv. In der Praxis sind bei Gütern häufig qualitative Unterschiede zu beobachten. Denkbar sind solche Unterschiede sowohl auf der Angebots-, als auch auf der Nachfrageseite (so unterscheiden sich die Nachfrager von Versicherungen durch ihr Risiko, etwa ihren Fahrstil). Beide Marktseiten können also heterogen sein.[2]
Um dennoch eine differenzierte Auswahl unter den Produkten zu haben, muß sich ein Wirtschaftssubjekt über die Qualität des Produktes informieren. Diese Möglichkeit hat jeder Marktteilnehmer, aber sie ist nicht kostenlos: Entgegen der " orthodoxen Wirtschaftstheorie, nach der Gütertausch ohne Ressourcenaufwand stattfindet, ist er tatsächlich mit Transaktionskosten verbunden. [] Transaktionskosten entstehen durch unvollkommene Information der am Güter- und Leistungsaustausch beteiligten Wirtschaftssubjekte."[3] Beispiele für Transaktionskosten sind Kosten, um sich über Qualitätsunterschiede heterogener Güter zu informieren, Kosten, Verträge abzuschließen oder Verträge zu überwachen.
Da Transaktionskosten sehr hoch sein können (eventuell sind Informationen gar nicht zu beschaffen, etwa wegen Datenschutz), können Situationen entstehen, in denen eine Marktseite über die Qualität des Produktes besser informiert ist als die andere. Ein klassisches Beispiel ist ein gebrauchtes Auto, wo der Vorbesitzer eventuelle Mängel seines Autos kennt, nicht aber ein potentieller Käufer (sofern er nicht gerade Automechaniker ist)[4]. Ist eine Marktseite von Informationsdefiziten stärker betroffen, herrscht eine asymetrische Informationsverteilung.
Ein extremes Beispiel für Informationsasymmetrie ist eine Person, die Lose verkauft und zufällig weiß, welche Lose gewinnen und welche nicht. Als rationales Wirtschaftssubjekt kauft der Verkäufer selbst die Gewinnlose und verkauft nur Nieten. So erzielt er einen Gewinn durch Ausnutzen seines Informationsvorsprungs.[5]
Die Principal-Agent-Theorie untersucht die vertraglichen Beziehungen zwischen zwei Parteien von Wirtschaftssubjekten:
einer Instanz mit niedrigem Informationsstand, die Prinzipal genannt wird, und
einem Entscheidungsträger mit hohem Informationstand, der Agent genannt wird.
Zwischen beiden herrscht eine asymmetrische Informationsverteilung. Der Agent verfügt über die Entscheidungsfreiheit, mit seinen Handlungen ist jedoch die Wohlfahrt des Prinzipals verknüpft. Besondere Beachtung verdienen Agency-Beziehung durch die folgenden zwei Eigenschaften.
Typisch für Agency-Beziehungen ist, daß der Prinzipal die Handlungen des Agenten nicht beobachten kann (hidden action). Dadurch kann der Entscheidungsträger Mißerfolge mit ungünstigen Umweltkonstellationen begründen und so Leistungsdefizite verbergen. "Da der Prinzipal annahmegemäß die Handlung des Agenten nicht beobachten kann, ist es nicht sinnvoll möglich, diese im Vertrag festzulegen".[7]Deshalb kann sich auch die Bezahlung nicht nach den Aktionen des Agenten richten.
Der Prinzipal kann nur versuchen, aufgrund des Ergebnisses auf die Handlungen des Agenten zu schließen, wobei vom Ergebnis nicht zweifelsfrei auf die Handlung geschlossen werden kann: Zwischen Ergebnis und Handlung besteht lediglich eine stochastische Beziehung, eine Handlung impliziert also kein bestimmtes Ergebnis. Insbesondere kann aus einem -aus der Sicht des Prinzipals- schlechten oder suboptimalen Ergebnis nicht zwingend auf mangelnden Einsatz des Agenten geschlossen werden.
Der Prinzipal verfügt nicht über die selben Informationen. Er kann zwar das Ergebnis beobachten, aber er hat einen zu geringen Kenntnisstand in bezug auf bestimmte "Qualitätsmerkmale" wie z.B. der Nutzenfunktion des Agenten (hidden information
Da der Agent die Entscheidungen trifft, kann er neben den Interessen des Prinzipals auch eigene verfolgen. Insbesondere wird er versuchen, seinen Arbeitseinsatz möglichst gering zu halten, da dieser als "disutility" (Arbeitsleid) in seine Nutzenfunktion eingeht. Man kann sagen, daß ein Kontrakt zwischen Agent und Prinzipal eine Ex-ante-Leistung des Prinzipals darstellt, die Aktionen bzw. der Arbeitseinsatz des Agenten jedoch eine Ex-post-Leistung.[8]
In der Realität lassen sich viele Agency-Beziehungen beobachten, z.B. zwischen Anwalt und Klient, Arzt und Patient, Auftraggeber und Werkstatt oder Schuldner und Gläubiger.
Moral hazard wird meistens mit "moralische Wagnisse" übersetzt. Auch moral hazard beruht auf ungleicher Verteilung von Informationen. Buchanan definiert moral hazard so: "Moral hazard is every deviation from correct human behavior that may pose a problem for an insurer."[9] Da diese Definition nicht aussagt, was unter "korrektem menschlichem Verhalten" zu verstehen ist, ist sie sehr allgemein. Genauer definiert Schumann: "Damit ist gemeint, daß Versicherte den Versicherungsfall vorsätzlich herbeiführen oder geringe Sorgfalt in der Vermeidung des Versicherungsrisikos walten lassen."
Noch präziser ist die Definition von Nell: Moral hazard nennt er " versicherungsinduzierte Verhaltensänderungen von Versicherungsnehmern, die dann und nur dann auftreten, wenn der Versicherer das Verhalten des Versicherungsnehmers und das exogene Risiko nicht getrennt beobachten kann."[11]
Das bedeutet: Während der Versicherte sein Risiko kennt, ist für die Versicherung die "Sorgfältigkeit" eines Individuums nicht meßbar, d.h. die Versicherung kann nicht hinreichend zwischen objektivem (="exogenem") Risiko einer Beschädigung und fahrlässigem Verhalten unterscheiden. Deckt sie das gesamte Risiko ab, erleiden Versicherte keinen Schaden, wenn sie sich nachlässig verhalten. Da Sorgfalt Geld oder Zeit kostet, werden rationale Individuen nach Abschluß einer Versicherung ihr Verhalten ändern und mit ihrem Eigentum weniger sorgfältig umgehen. Da Versicherte ihre Sorgfalt nach Abschluß der Versicherung einschränken, erhöhen sie damit die Wahrscheinlichkeit, daß ein Schadensfall auftritt. Sie befinden sich in einer Situation des moral hazards.
In einem Dorf mit 100 Hausbesitzern beträgt der Wert jedes Hauses 100.000 DM.[12] Die Wahrscheinlichkeit, daß ein Haus innerhalb einer Periode abbrennt und dadurch völlig zerstört wird, ist 1%. Die Bewohner kennen die Wahrscheinlichkeit, wissen aber nicht, welches Haus als nächstes zerstört wird.
Ein Hausbesitzer wird bereit sein, 1000 DM (100.000 DM*0,01) in eine gemeinsame Kasse zu bezahlen, um denjenigen, dessen Haus zerstört wurde, zu entschädigen. So geht der Verlust im Brandfall auf 1000 DM zurück (die Zahlung in die Gemeinschaftskasse).
Eine Firma zur Brandbekämpfung macht einem Hauseigentümer jetzt ein Angebot: Durch Schutzmaßnahmen wird die Wahrscheinlichkeit des Feuers von 1% auf 0,5% reduziert. Ohne Versicherung wäre dem Hauseigentümer das Angebot mindestens 500 DM wert (100.000 DM*0,005).
Ist der Hausbesitzer versichert, sinkt seine Zahlungsbereitschaft auf 5 DM (1000 DM*0,005), denn falls ein Haus abbrennt, zahlt er ja nur die Versicherungsprämie von 1000 DM. Sein Interesse an Feuerschutzmaßnahmen ist gesunken; der Hauseigentümer hat weniger Anreiz, auf sein Eigentum zu achten, als wenn keine Versicherung bestünde. Nach Abschluß der Versicherung ändert sich sein Verhalten.
Versicherungen können auch dazu führen, daß die Nachfrage der Versicherten nach dem versicherten Gut ansteigt. Beispiel Krankenversicherung: Ohne Versicherung hat jedes Individuum eine bestimmte Nachfrage nach ärztlichen Leistungen. Bezahlt nun eine Versicherung alle Kosten, so bezahlt der Versicherte -neben der Versicherungsprämie- nichts mehr. Als Folge dieser Verbilligung werden mehr oder teurere Leistungen nachgefragt; ist das Angebot starr, so steigen die Preise.
In den USA fiel bei Krankenversicherungen der Anteil der Selbstbeteiligung zwischen 1950 und 1974 von 35% auf 10%. In dieser Zeit stieg der Konsumentenpreisindex um 122%, der Preisindex für medizinische Leistungen dagegen um 700%.[13]
Auch in Betrieben finden sich Situationen des moral hazard. Eine Aktiengesellschaft besteht vereinfacht aus Kapitalgebern und Management.[14] Die Interessen beider Gruppen sind möglicherweise nicht gleich: Ziel der Eigentümer ist eine hohe Verzinsung ihres Kapitals, d.h. ein hoher Gewinn. Das Management verfolgt neben der Erzielung eines hohen Gewinns eventuell noch eigene Ziele wie teure Reisen auf Firmenkosten, teure Firmenwagen und andere persönliche Vergünstigungen.
Diese Vergünstigungen schmälern den Gewinn der Unternehmung, erhöhen aber den Nutzen des Managers. Besitzt der Manager Aktien der Unternehmung, etwa 1% des Wertes der Firma, dann verringert sich sein Gewinn nur um einen Pfennig, wenn er eine Mark für persönliche Vergünstigungen ausgibt.
Arbeiter haben bei Einstellungsgesprächen Anreiz, ihre Leistungen überzubewerten, um eingestellt zu werden. Im Arbeitsleben wird ihre Leistungsbereitschaft sinken, da Arbeitseinsatz negativ in ihre Nutzenfunktion eingeht. Nach Vertragsschluß ändern sie also ihr Verhalten und schaden damit dem Unternehmen (auch als shirking ("Drückebergerei") bezeichnet).
In diesem Abschnitt wird in enger Anlehnung an Nell (1993) formal und graphisch untersucht, wie eine Versicherung das Verhalten des Versicherten beeinflußt.
Ein risikoaverses Wirtschaftssubjekt steht vor der Entscheidung, sich gegen ein bestimmtes Risiko versichern zu lassen. Der erwartete Nutzen bestimmt sich nach dem Bernoulli-Kriterium, nach dem für verschiedene Umweltzustände eine "Nutzenfunktion für die Konsequenzen" [15] zwischengeschaltet wird:
E[U(x)] = p1*U(x1) + p2*U(x2) + p3*U(x3) +
Zu Beginn der Periode besitzt das Individuum ein Vermögen w; mit einer Wahrscheinlichkeit p kommt es während der Periode zu einem Schaden in Höhe von D. Durch präventive Maßnahmen kann das Wirtschaftssubjekt die Höhe des Schadens beeinflussen, nicht aber die Schadenswahrscheinlichkeit p. Diese präventiven Maßnahmen (etwa vorsichtige Fahrweise) können bewertet werden durch ein "Maß für das Schadensverhütungsniveau" s. Nicht möglich ist es, die Schadenshöhe auf Null zu setzen. Die präventiven Maßnahmen sind für das Wirtschaftssubjekt mit Kosten c verbunden.
Unterstellt wird eine abnehmende Grenzwirkung der Schadensverhütung, D=D(s) mit D´(s) < 0 und D´´(s) > 0, sowie steigende Grenzkosten der Schadensverhütung, c=c(s) mit c´(s) > 0 und c´´(s) > 0.
Beim optimalen Maß an Schadensverhütung wird das Wirtschaftssubjekt den erwarteten Nutzen seines Vermögens am Ende der Periode maximieren:
maxs E(u) = (1-p)*U[w - c(s)] + p*U[w - D(s) - c(s)]
Ableiten ergibt die Bedingung erster Ordnung für das optimale Schadensverhütungsniveau:
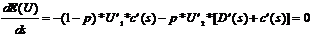
mit U1 = U[w-c(s)] und U2 = U[w-D(s)-c(s)]. [16]
So ergibt sich das Maß für die optimale Schadensverhütung zu:
Gleichung
Im Optimum der Schadensverhütung entsprechen die Grenzkosten dem Grenzertrag der Schadensverhütung. Der Grenzertrag der Schadensverhütung ist dabei die marginale Verringerung der Schadenshöhe, gewichtet mit der Schadenswahrscheinlichkeit.
Mit steigendem Grad der Risikoaversion steigt der Grenzertrag der Schadensverhütung (ausgedrückt durch die Bernoulli-Nutzenfunktion). Daher wird ein Wirtschaftssubjekt um so mehr präventive Maßnahmen ergreifen, je risikoscheuer es ist.
Die Risikosituation kann im Modell mit Versicherung auf zwei Weisen beeinflußt werden: Das Wirtschaftssubjekt kann neben der Höhe seiner eigenen Schadensvorsorge über die nachgefragte Menge an Versicherungsschutz entscheiden.
a sei der Deckungsgrad der Versicherung, d.h. derjenige Teil des Schadens, der durch die Versicherung abgedeckt ist; 1-a der Selbstbehalt des Versicherten (etwa Selbstkostenbeteilung bei der Vollkaskoversicherung). Annahmegemäß kann der Versicherer das Verhalten des Versicherungsnehmers beobachten und verlangt eine Versicherungsprämie, die proportional ist zum erwarteten Schaden. Sie beträgt q*a*p*D, wobei q einen Zuschlag darstellt, um die Betriebskosten des Versicherers zu decken.
Das Maximierungskalkül des Wirtschaftssubjektes wird damit zu:
maxs, a E(u) = (1-p)*U[w - apqD(s) - c(s)] + pU[w - apqD(s) - (1-a)D(s) - c(s)]
Die beiden Bedingungen erster Ordnung für eine innere Lösung sind:
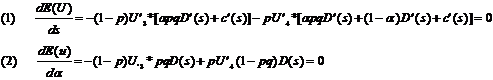
Gleichung
mit U3 = U[w - apqD(s) - c(s)] und U4 = U[w - apqD(s) - (1-a)D(s) - c(s)].
Die optimale Schadensverhütung ergibt sich aus Gleichung 2/(1) zu:
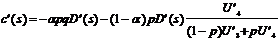
Gleichung
Berücksichtigt man, daß aus Gleichung 2/(2) folgt:
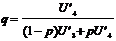
Gleichung
so läßt sich Gleichung 3 vereinfachen zu:
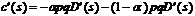
Dies ist gleich:
c´(s)=-pqD´(s)
Gleichung
Im Optimum sind die Grenzkosten der Schadensverhütung gleich der marginalen Anderung der Versicherungsprämie (die wiederum ja proportional war zum erwarteten Schaden). Dies ist unabhängig vom Grad der Risikoscheu, da die individuelle Nutzenfunktion nicht als Argument auftritt. Graphisch läßt sich Gleichung 5 so darstellen:
Abbildung : Grenzkosten und Grenzertrag der Schadensverhütung
Die Grenzkosten der Schadensverhütung steigen mit zunehmender Sorgfalt. Mit zunehmender Sorgfalt sinkt aber auch die Schadenswahrscheinlichkeit und damit auch die Versicherungsprämie. Das optimale Maß der Schadensverhütung ist dann durch den Schnittpunkt bestimmt.
Im vorigen Abschnitt zeigte sich, daß der Grad der Risikoaversion keinen Einfluß auf die Schadensverhütung ausübt, wenn Versicherungsschutz nachgefragt wird. Ohne Versicherung steigen die Ausgaben für präventive Maßnahmen, je risikoscheuer das Wirtschaftssubjekt ist. Jetzt soll gezeigt werden, daß Versicherungsschutz zu einer Verringerung der Schadensverhütung führt, mithin zu moral hazard
Damit das der Fall ist, muß gelten:
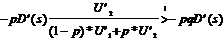
Dafür läßt sich -unter Berücksichtigung von Gleichung 4- schreiben:
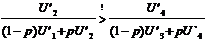
Umformen ergibt folgende Bedingung:
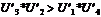
Gleichung
U1 bzw. U3 ist der Nutzen im Nicht-Schadensfall, U2 bzw. U4 der Nutzen im Schadensfall (jeweils ohne und mit Versicherung). "U1 muß größer sein als U3, da ohne Versicherung auch keine Versicherungsprämie gezahlt wird und U4 ist größer als U2, da Versicherung zu einer verbesserten Vermögensposition im Schadensfall führt."[17] Gleichung 6 ist damit für konkave Nutzenfunktionen immer erfüllt.
Das bedeutet: Der Grenzertrag präventiver Maßnahmen ist ohne Versicherung höher als mit Versicherung. Deshalb betreibt ein versichertes Wirtschaftssubjekt c.p. weniger Schadensverhütung als ein unversichertes. Graphisch läßt sich dies so verdeutlichen:
Abbildung : Die Höhe der optimale Schadensverhütung mit und ohne Versicherungsschutz
Da die Möglichkeit der Versicherung den Grenzertrag präventiver Maßnahmen senkt, sinkt auch das optimale Maß an Schadensverhütung. Ein risikoaverses Wirtschaftssubjekt zieht einen höheren Grenznutzen aus der Schadensvorsorge, deshalb würde es ohne Versicherung noch mehr Schadensverhütung betreiben als ein risikoneutrales.
Damit ist gezeigt, daß in diesem Modell das Vorhandensein von Versicherungsschutz Anderungen im Verhalten der Wirtschaftssubjekte impliziert. Ihre Maßnahmen zur Schadensverhütung nehmen ab, d.h. sie haben Anreiz, nach Vertragsschluß ihr Verhalten zu ändern und damit Anreiz zum moral hazard
Allokativ ist diese versicherungsinduzierte Verringerung der Schadensverhütung in diesem Modellrahmen positiv zu beurteilen: Der Versicherer kann ja (gemäß Annahme) die Schadensverhütungsaktivitäten beobachten und bei der Prämiengestaltung berücksichtigen. Er steht also der Verringerung an Schutzmaßnahmen indifferent gegenüber. Der Versicherungsnehmer dagegen verbessert sich durch die Verringerung an Schadensverhütung. Daher führt die Verringerung zu einer Pareto-Verbesserung.[18]
Am Beispiel des Losverkäufers (siehe Informationsasymmetrie) läßt sich demonstrieren, wie adverse selection (=Negativauslese) wirkt: Weiß ein potentieller Loskäufer, daß ihm nur noch Nieten angeboten werden, dann wird er kein Los kaufen. Der Absatz dieser Lotterielose wird auf Null zurückgehen und das Geschäft verschwinden.
"Klassisches Beispiel" für adverse Selektion ist der Markt für Gebrauchtwagen. Durch den Prozeß der Selbstauslese kann die Qualität der angebotenen Wagen negativ beeinflußt werden.[19]
Bei moral hazard und adverse selection verhindert Informationsasymmetrie, daß beide Marktparteien sachliche Präferenzen bilden können. Beidemal erscheint das Warenangebot homogen, obwohl tatsächlich unterschiedliche Qualitäten auftreten. Moral hazard und adverse selection sind zwei "verwandte" Phänomene, was sich z.B. bei freiwilligen Versicherungen zeigt, etwa der Unfallversicherung: Sind die Prämien hoch, dann lassen sich nur Personen mit hohem Risiko versichern. Es findet also eine Negativauslese statt.[20] In einer zweiten Phase, nach Vertragsschluß, haben sie zusätzlich Anreiz, ihr Verhalten zu ändern und so das Versicherungsrisiko weiter zu erhöhen: Das wäre dann ein moralisches Wagnis.
Beide Phänomene unterscheiden sich im Selektionsmechanismus: Kennzeichnend für moral hazard ist, daß erst nach dem Vertragsabschluß Anreiz besteht, das Verhalten zu ändern und damit die Qualität der Leistung negativ zu beeinflussen. Im Unterschied dazu steht bei adverse selection bereits bei Vertragsabschluß die Qualität der Leistung fest, die negative Auslese findet also vor Vertragsschluß statt.[21]
Um das Problem des moral hazard zu entschärfen, könnte die höhere Instanz (der Prinzipal) Kontrollen durchführen. Dies erfordert jedoch einen hohen Aufwand an Transaktionskosten zur Beschaffung von Informationen, die zur Beurteilung des Entscheidungsverhaltens nötig wären. Außerdem ist zu vermuten, daß -etwa bei moral hazard in Unternehmen - zu starke Kontrollen motivationshemmend auf die Mitarbeiter wirken.
Deshalb ist man bemüht, Anreize (Incentives) zu schaffen, um moral hazard zu vermeiden. Diese Anreize sollen das Verhalten der anderen Partei so beeinflussen, daß sie sich effektiv (oder allgemein auf eine erwünschte Weise) verhalten. Incentives müssen also so gestaltet sein, daß es von vornherein im Interesse des Agenten liegt, den Vertrag im Sinne des Prinzipals zu erfüllen.
In der Realität sind viele Anreizsysteme zu beobachten. Anreizwirkungen sollen z.B. von folgenden Maßnahmen ausgehen:
a) Vorsorgeuntersuchungen, die das Risiko einer Erkrankung mindern, führen bei der Krankenversicherung zu Beitragssenkungen. Ein Wirtschaftssubjekt hat also Anreiz, nicht wegen jeder Kleinigkeit zum Arzt zu gehen.
b) Vertreter werden nicht pauschal, sondern nach Leistung (Umsatz, "Punkteprämien") bezahlt. Nur wer fleißig arbeitet, verdient viel.
c) Belegschaftsaktien sollen Mitarbeiter zu besseren Leistungen motivieren: Da sie am Gewinn der Unternehmung über Aktienbesitz partizipieren, haben sie Anreiz, durch effektive Arbeit zu einem hohe Gewinn beizutragen.
d) Im Straßenverkehr besteht Anreiz, vorsichtig zu fahren: Mit jedem unfallfreien Jahr reduziert sich die Versicherungsprämie.
e) Eine Selbstkostenbeteiligung bei Versicherungen führt dazu, daß sie nicht bei jedem Bagatellfall in Anspruch genommen wird.
Bei der Schaffung von Anreizen ist der Grad der Risikoaversion beider Parteien ein entscheidender Faktor, da sich bei Risikoaversion die Übernahme eines Risikos negativ auf die Wohlfahrtsposition des Wirtschaftssubjektes auswirkt.
In diesem Abschnitt wird in enger Anlehnung an Ruhl (1990) formal und graphisch untersucht, wie optimale Anreizsysteme bei Arbeitsverträgen aussehen können.
Ein Prinzipal überträgt einem nachgeordneten Entscheidungsträger Aufgaben. Der Erfolg G setzt sich zusammen aus der Leistung des Entscheidungsträgers x und einer stochastischen Komponente q:
G = f(x) + q.
Die Störvariable q sei dabei N(0, s )-verteilt und repräsentiert nicht beeinflußbare Umweltfaktoren. Der Erfolg G ist damit ebenfalls eine normalverteilte Zufallsvariable.
Der erwartete Nutzen des Prinzipals ergibt sich als:
E,
dabei ist U(x) der Nutzen und E(U) der erwartete Nutzen des Prinzipals, P(G) ist die Prämienfunktion.
Der Agent wählt ein Leistungsniveau x*, das seinen Erwartungswert aus Nutzen der Prämie P und Leistung maximiert. Er arbeitet ungern, so daß seine Nutzenfunktion den Arbeitseinsatz als negatives Argument enthält.
Das Arbeitsleid wird wie negatives Einkommen bewertet und in Geldeinheiten ausgedrückt. Es nimmt mit steigendem Arbeitseinsatz zu. E(V) ist der Erwartungswert des Nutzens des Agenten, der sich aus dem Nutzen der erhofften Prämie und des Arbeitsleids L(x) zusammensetzt:
E(V) = E - L(x*).
Damit der Prinzipal seinen erwarteten Nutzen maximieren kann, muß er die Reaktionen des Agenten antizipieren. Ein höheres Arbeitsniveau des Agenten bewirke eine vorteilhaftere Wahrscheinlichkeitsverteilung über den Erfolg: je mehr (intensiver) der Agent arbeitet, desto wahrscheinlicher werden größere Erfolge. Eine Prämie erhält der Agent, falls sein Erfolg über einen -vom Prinzipal vorgegebenen- Soll-Erfolg SG hinausgeht. In diesem Fall steigt die Prämie mit dem tatsächlich erzielten Erfolg:
P(G) = p(G-SG),
Gleichung
wobei p den Prämiensatz angibt. Die Prämienfunktion ist anreizkompatibel: Der Erwartungswert der Prämie E[P] ist eine monoton steigende Funktion des erwarteten Netto-Erfolges des Prinzipals E[G-P].
Außerdem wird dem Agent in jedem Fall ein Mindestnutzen in Höhe von VM gewährt als Schutz vor zu hoch angesetzten Soll-Erfolgen.
Der Agent maximiert seinen Nutzen, indem er sein Leistungsniveau wählt. Bei Risikoneutralität ergibt sich in Verbindung mit der Prämienfunktion (Gleichung 7):
Maxx E(V) = p - L(x)
Differenzieren und Nullsetzen ergibt:
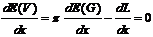
Gleichung
Der Entscheidungsträger wählt sein Leistungsniveau so, daß im Optimum der erwartete Grenzertrag der Prämie gleich dem Grenzarbeitsleid ist. Der Soll-Erfolg SG beeinflußt das Verhalten des Agenten nicht. Mit steigendem Prämiensatz steigt auch seine Leistung, er besitzt also folgende Reaktionsfunktion:
x(p) mit dx/dp>0.
Gleichung 9
Ziel des Prinzipals ist die Maximierung seines Netto-Ertrages. Für sein Maximierungskalkül läßt sich eine Lagrange-Funktion aufstellen (mit m als Lagrange-Multiplikator), wenn man zu seinem erwarteten Netto-Erfolg als Nebenbedingung die Prämie des Agenten berücksichtigt. Dann lautet das Maximierungskalkül des Prinzipals in Verbindung mit der Reaktionsfunktion des Agenten (Gleichung 9):
Maxp, SG, m F = (1-p)*E[G(x*(p))] + pSG + m[VM - p + L(x*(p))].
Partielles Ableiten und Nullsetzen ergibt:
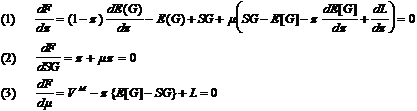
Gleichung
Gleichung 10/(2) ergibt: m*=-1. Daraus folgt, "daß der Nutzen der Instanz um eine marginale Einheit fällt, wenn der Mindestnutzen des Entscheidungsträgers VM um eine marginale Einheit ansteigt." Dies ist nicht verwunderlich, da VM in jedem Fall gewährt wird.
m* in Gleichung 10/(1) eingesetzt ergibt:
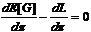
Gleichung
Leitet man dE/dp und dL/dp nach der Kettenregel ab, dann ergibt sich aus Gleichung 11:
.
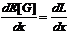Im Optimum ist Gleichung 8 stets erfüllt, so daß man dL/dx wie folgt ersetzen kann:
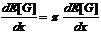
Gleichung 12
Direkt abzulesen ist dann der aus Sicht des Prinzipals optimale Prämiensatz:
p*=1
Gleichung 13
Ist der Prämiensatz p*=1, dann gilt: "Die Instanz überläßt dem Entscheidungsträger bei Risikoneutralität den gesamten Erfolg, der den optimalen Soll-Erfolg SG* übersteigt []". Arbeitet der Agent also besser als vom Prinzipal vorhergesehen, darf er den gesamten zusätzlichen Erfolg behalten.
Der optimale Soll-Erfolg SG* ergibt sich, indem man Gleichung 11 in Gleichung 10/(3) einsetzt:
SG*=E[G]*-L*-VM.
Gleichung 14
"Der Soll-Erfolg SG* entspricht im Optimum gerade dem Erwartungswert des Erfolges, vermindert um das Arbeitsleid und den Mindestnutzen VM des Entscheidungsträgers für p*=1."
Das heißt: Der Prinzipal bestimmt zunächst den optimalen Soll-Erfolg. Dieser ergibt sich aus dem Erwartungswert des Erfolges, abzüglich dem Arbeitsleid des Agenten und dessen Mindestnutzen. Übersteigt der tatsächlich erzielte Erfolg den Soll-Erfolg, so erhält der risikoneutrale Agent eine Prämie mit Prämiensatz p* = 1, d.h. er erhält den gesamten zusätzlichen Erfolg.
Das Maximierungskalkül des Prinzipals läßt sich nach Ruhl (1990) auch graphisch verdeutlichen.
Da verstärkte Anstrengungen des Agenten den Erfolg positiv beeinflussen, verläuft der Graph des erwarteten Gewinnes in Abhängigkeit von der Leistung des Agenten konkav und monoton wachsend. Da die Prämie linear vom erwarteten Gewinn abhängt, verläuft auch sie konkav und monoton wachsend.
Die Nutzenfunktion des Agenten bestimmt, wie er mit seiner Leistung x auf unterschiedliche Prämien reagiert. Seine Indifferenzkurven geben an, welche Kombinationen von Leistung und erwartete Prämie er als gleichwertig einstuft. Da eine Leistungssteigerung bei gleichem Nutzenniveau einen überproportionalen Anstieg der Prämie zur Folge hat, verlaufen die Indifferenzkurven konvex. Bewegt man sich im Indifferenzkurvensystem nach oben, steigt das Nutzenniveau. Graphisch läßt sich das so darstellen:
Abbildung : Wie wirkt ein steigender Prämiensatz auf die Leistung?
Den Anpassungspfad erhält man, indem man die Tangentialpunkte der erwarteten Prämien und der Indifferenzkurven verbindet. Er beschreibt, wie alternative Prämiensätze auf die Leistung des Agenten wirken. Trägt man den Anpassungspfad mit dem Graph des Erwartungswertes des Erfolges E[G(x)] in ein neues Schaubild ein und berücksichtigt, daß der Anpassungspfad um den Mindestnutzen VM nach oben verschoben werden muß, so ergibt sich:
Abbildung : Der optimale Prämiensatzes bei Risikoneutralität
Der Prinzipal wählt jenen Prämiensatz, bei dem der vertikale Abstand zwischen erwartetem Erfolg und Anpassungspfad maximal wird. Die optimale Prämienfunktion ist dann durch p* determiniert.
Behandelt wird Risikoaversion des Agenten bei Risikoneutralität des Prinzipals. Das Entlohnungsprinzip wird beibehalten, da lineare Prämienfunktionen in der Realität oft eingesetzt werden. Der Prinzipal muß aber beachten, daß der Agent einen Ausgleich fordert für das übernommene Risiko.
Hierzu stellt er dem Agenten ein Sicherheitsäquivalent zur Verfügung: "Das Sicherheitsäquivalent stellt dabei jenen sicheren Zielgrößenwert dar, den der Entscheidungsträger als gleichwertig mit der Wahrscheinlichkeitsverteilung über die Prämie betrachtet"[27]. Anders ausgedrückt: Da der Agent risikoscheu ist, schätzt er den Nutzen der erwarteten Prämie geringer ein. Das Sicherheitsäquivalent gibt an, welchen Nutzen der Agent der erwarteten Prämie beimißt:
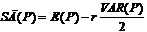, mit r > 0.
r ist ein Parameter, der den Grad der Risikoaversion des Agenten angibt und VAR(P) die Varianz der Prämie. Für sie gilt: VAR(P) = p s , wobei s die Varianz des Erfolges angibt und nicht von der Leistung des Agenten beeinflußt wird.
Der erwartete Nutzens des Agenten E(V) ergibt sich aus Sicherheitsäquivalent und Arbeitsleid (das wieder wie negatives Einkommen in Geldeinheiten bewertet wird):
E(V)=SA(P) - L(x) = VM.
Dies stellt gleichzeitig seinen Mindestnutzen dar.
Der Agent maximiert den Erwartungswert des Nutzens bezüglich seiner Leistung. Es gilt also:
Maxx
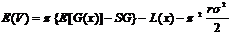
Die notwendige Bedingung ist dann:
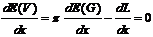
Gleichung 15
Analog zu Gleichung 8 ist wieder das Leistungsniveau optimal, bei dem der erwartete Grenzertrag der Prämie gleich dem Grenzleid der Arbeit ist. Weder der Soll-Erfolg SG, noch der Grad der Risikoscheu r oder die Varianz des Erfolges s beeinflussen das Anpassungsverhalten.
Der Anreizeffekt der Prämie bleibt erhalten, denn auch hier steigt die Leistungsbereitschaft des Agenten an, wenn die Prämie ansteigt. Für seine Reaktionsfunktion x*(p) gilt also wieder dx*/dp > 0.
Der Prinzipal möchte auch weiterhin seinen Netto-Erfolg maximieren. In Verbindung mit der Prämien- und der Reaktionsfunktion des Agenten sieht sein Kalkül jetzt so aus:
Maxp, SG, m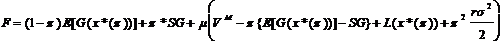 
Die notwendige Bedingung ergibt sich durch partielle Differentiation:
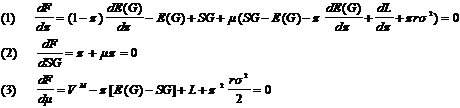
Gleichung
Aus Gleichung 16/(2) ergibt sich: m*=-1. Eingesetzt in Gleichung 16/(1) erhält man:
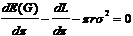
Leitet man
dL/d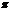
wieder nach der Kettenregel ab und beachtet, daß im Optimum
des Agenten das Grenzleid der Arbeit dem marginalen erwarteten Prämienertrag
entspricht (Gleichung
15), so ergibt sich:
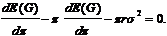
Daraus läßt sich der optimale Prämiensatz ermitteln:
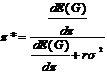
Gleichung 17
Für 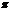* gilt: 0 < 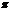* < 1, da dE[G]/dp > 0 und
rs > 0. Bei Risikoaversion des Agenten ist
also der Prämiensatz grundsätzlich niedriger.
dE(G)/dp gibt an, wie der erwartete Grenzerfolg auf Anderungen der Prämie reagiert. Der optimale Prämiensatz ist um so höher, je größer dE(G)/dp ist, d.h. je leistungsmotivierender ein hoher Prämiensatz auf den Agenten wirkt.
Ist der
dE(G)/dp
gegeben, so ist "der optimale
Prämiensatz 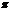* [] um so größer, je kleiner der
Risikoaversions-Koeffizient r und je kleiner die Varianz des Erfolgs s ist[28]".
Je größer also die Risikobereitschaft des Agenten ist, desto mehr kann er
verdienen, weil der Prämiensatz ansteigt, oder umgekehrt: Je geringer die
Risikobereitschaft, desto weniger hängt die Bezahlung des Agenten vom Erfolg
ab, sondern tendiert mehr und mehr in Richtung einer fixen Bezahlung in Höhe
von VM. Je "fixer" die Bezahlung ist, desto geringer ist das Risiko
des Agenten und desto mehr übernimmt der Prinzipal das Risiko.
Je geringer die Streuung des Erfolges ist, desto geringer streut auch die Prämie. Das Risiko des Agenten nimmt also ab. Deshalb wird er bei geringer Varianz des Erfolges stärker am Risiko beteiligt.
Hat man den optimalen Prämiensatz p* ermittelt, so ergibt sich der Soll-Erfolg im Optimum SG*, indem man x* aus Gleichung 15 in Gleichung 16/(3) einsetzt:
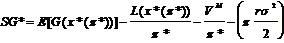
Gleichung
Da 0 < p* < 1, ist der Inhalt der Klammer positiv. Vergleicht man also diesen Soll-Erfolg mit Gleichung 14, so stellt man fest, daß er bei einem risikoscheuen Agenten geringer ist. Die Anforderungen des Prinzipals an risikoscheue Agenten sind also geringer.
Analog zu Abbildung 4 wird eine konkave Kurve des erwarteten Erfolges E[G(x)] angenommen.
Der Anpassungspfad in Abbildung 4 gab an, wie alternative Prämiensätze auf die Leistung des risikoneutralen Agenten wirkten. Hier ist der Agent risikoavers, er fordert zusätzlich eine Risikoprämie in Höhe von R=½p rs . Zu dem Anpassungspfad muß also die Risikoprämie addiert werden.
Der Verlauf der neuen Kurve wird wie folgt konstruiert: Nimmt man einen Prämiensatz von p=1 ein, so beträgt die Risikoprämie noch R=½rs . Senkt man p, so sinkt auch die Risikoprämie; im Extremfall p=0 ist R=0: Wird keine Erfolgsprämie gezahlt, ist die Bezahlung konstant und das Risiko des Agenten gleich Null. So läßt sich eine Anpassungskurve mit Risikoprämie konstruieren, die um so steiler verläuft, je risikoscheuer der Agent ist. Ist rs =0, ist der Anpassungspfad mit Risikoprämie identisch mit dem Anpassungspfad aus Abbildung 4. Graphisch sieht das so aus:
Abbildung 5: Das optimale Leistungsniveau bei Risikoaversion des Agenten
Analog zu Abbildung 4 ist beim optimalen Leistungsniveau des Agenten x* der Abstand zwischen Gewinn und Bezahlung des Agenten maximal. Die Risikoprämie R* ergibt sich dann als Aufschlag aus dem Abstand zwischen Anpassungspfad mit und ohne Risikoprämie beim optimalen Leistungsniveau. Sie ist abhängig vom Grad der Risikoaversion.
An dieser Stelle scheint es mir angebracht, einige der getroffenen Annahmen kritisch zu reflektieren. Wenig praxisrelevant ist wohl, daß im Modell die Wahrscheinlichkeitsverteilung der Ergebnisse genau bekannt ist. Eine exakte Spezifizierung der Verteilung würde bedeuten, daß der Prinzipal detaillierte Informationen über die Konsequenzen der Aktionen des Agenten hat und daß er ihn völlig richtig einschätzt.
In der Realität wird es wohl eher so sein, daß Prinzipal und Agent die Wahrscheinlichkeitsverteilungen individuell schätzen. Stimmen beide Parteien nicht in ihren Fähigkeiten, ihrem Kenntnisstand oder in ihrem Grad der Risikoaversion überein, werden die Schätzungen im allgemeinen unterschiedlich ausfallen. Da aber das gesamte Maximierungskalkül auf einer (von beiden gleich angenommenen) Wahrscheinlichkeitsverteilung aufbaut, ist die Übereinstimmung von zentraler Bedeutung. Dies ist eindeutig eine Schwäche dieses Ansatzes.
Für problematisch halte ich in diesem Zusammenhang auch, daß der Grad der Risikoaversion durch einen Parameter angegeben wird. Unklar ist, wie dieser Parameter bestimmt werden soll und ob Agent und Prinzipal den Grad der Risikoaversion gleich bewerten.
In den vorstellten Ansätzen war den Schwierigkeitsgrad der Aufgabe bekannt. In der Realität verändert sich oft der Schwierigkeitsgrad (bzw. dessen Einschätzung) beim Bearbeiten einer Aufgabe. Auch wird völlige Konstanz der Eigenschaften des Agenten angenommen. Damit bleibt ausgeschlossen, daß er bei der Bearbeitung des Auftrages "dazulernt", also seine Effektivität steigert.
Dagegen ließe sich argumentieren, daß der Prinzipal die Leistung des Agenten zu Beginn einschätzt und mit seiner Schätzung richtig liegt. Dies impliziert allerdings wiederum, daß der Prinzipal den Agenten sehr genau kennt. Weiter verfeinern ließen sich die Modelle, wenn man zu einer Mehrperiodenbetrachtung übergeht. Allerdings sind bereits die vorgestellten Schemen recht kompliziert und stehen damit im Gegensatz zu den eher einfach strukturierten Anreizsysteme in der Realität.
Trotz dieser Kritik bleibt festzuhalten, daß es Anreizmöglichkeiten gibt, mit denen moral hazard gemindert wird. Auch wenn man mit den vorgestellten Anreizstrukturen wegen zusätzlicher Verzerrungen der Realität kein optimales Ergebnis erreicht, so begrenzen sie trotzdem das Risiko der Versicherung oder des Arbeitgebers.
Eine Unternehmung vertreibt ihr Produkt über einen Vertreter. Der Vertreter, der sonst kein Einkommen bezieht, muß sich entscheiden, wie sehr er sich für diesen Auftrag engagieren möchte: stark oder weniger stark (ausgedrückt durch hohe oder niedrige Arbeitsintensität). Setzt er sich sehr für das Produkt ein, wird die Herstellerfirma stärker von seiner Arbeit profitieren, als wenn er sich nur mäßig engagiert. Die Firma hat keine Möglichkeit, das Verhalten ihres Vertreters zu beobachten. Als Ergebnis seiner Tätigkeit erhält sie lediglich die Menge an zusätzlichen Aufträgen. Im Beispiel gebe es drei Möglichkeiten, deren Wahrscheinlichkeiten von der Arbeitsintensität des Agenten beeinflußt werden:
|
Wahrscheinlichkeit für: |
geringe Intensität |
hohe Intensität |
|
keine zusätzlichen Aufträge |
|
|
|
Aufträge im Wert von 250 DM |
|
|
|
Aufträge im Wert von 750 DM |
|
|
Tabelle : Die Wahrscheinlichkeit der Ereignisse
Die Zuordnung ist nicht eindeutig, so führt eine hohe Arbeitsintensität nicht automatisch zu Aufträgen im Wert von 750 DM. Die Firma kann bei Aufträgen im Wert von 750 DM nur schließen, daß eine hohe Arbeitsintensität wahrscheinlicher war. Weil der Prinzipal die Aktion des Agenten nicht beobachten kann und außerdem jede Aktion zu jedem Ergebnis führen kann, kann der Vertrag zwischen Agent und Prinzipal keine Bezahlung in Abhängigkeit von der Arbeitsintensität enthalten. Für den Agent bestünde bei fixer Bezahlung die Versuchung, die am wenigsten beschwerliche Aktion zu wählen. Dies versucht der Prinzipal durch eine geeignete Anreizstruktur zu verhindern.
Der Agent ist risikoneutral. Sein Nutzen ergibt sich als Funktion seines Gehaltes w und der Arbeitsintensität a. Seine Nutzenfunktion sei U(w,a) = w - a.
Seine Arbeitsintensität wird wieder in Geldeinheiten (hier DM) umgerechnet (vgl. Seite 1), er wählt zwischen "gering" (a=75) und "hoch" (a=100). Sein Minimalnutzen ist VM=100.
Soll sich der Vertreter also mit hoher Arbeitsintensität engagieren, muß dies der Firma mindestens 200 DM wert sein, damit der Agent seinen Minimalnutzen erreicht. Damit der Agent überhaupt für die Firma tätig wird, muß sie ihm 175 DM bezahlen.
|
geringe Intensität |
hohe Intensität |
|
|
zu erreichender Minimalnutzen VM: |
|
|
|
+ Arbeitsintensität a: |
|
|
|
= von der Firma zu zahlen, damit der Vertreter für sie arbeitet |
|
|
Tabelle : Die Bezahlung des Agenten
Auch der Prinzipal ist risikoneutral.
Der Nutzen der Unternehmung ergibt sich aus der Aktion des Agenten. Wenn der Vertreter mit geringer Intensität arbeitet, so beträgt der erwartete Brutto-Gewinn des Unternehmens 0,6*0 + 0,3*250 + 0,1*750 = 150 DM, arbeitet er mit hoher Intensität, so beträgt der erwartete Brutto-Gewinn 525 DM.
Die Firma wird den Vertreter engagieren, wenn er mit hoher Intensität arbeitet, denn dann macht sie einen erwarteten Netto-Gewinn von 325 DM. Falls jedoch von Beginn an feststeht, daß er nur mit 'geringer Intensität' arbeitet, erleidet sie einen (erwarteten) Schaden von -25 DM; noch größer wird der Schaden, falls sie ihm für hohe Intensität 200 DM bezahlt, er aber nur mit geringer Intensität arbeitet. Der maximal erzielbare Netto-Gewinn der Unternehmung beträgt 325 DM.
|
geringe Intensität |
hohe Intensität |
|
|
erwarteter Bruttogewinn der Unternehmung |
150 DM |
525 DM |
|
- Zahlung an den Vertreter |
-175 DM |
-200 DM |
|
= erwarteter Nettogewinn der Unternehmung |
-25 DM |
325 DM |
Tabelle 3: Das Kalkül der Unternehmung
Der Prinzipal wird versucht sein, Anreize zu schaffen, daß der Agent mit hoher Intensität arbeitet. Dies soll durch den Arbeitsvertrag geschehen. Die Gleichungen für die optimale Prämienfunktion bei Risikoneutralität (Gleichung 13 und Gleichung 14) geben vor, wie die Anreize auszusehen haben.
Die Firma vereinbart folgendes: 'Wenn kein zusätzlicher Auftrag eingeht, muß der Vertreter 325 DM bezahlen. Gehen Aufträge im Wert von 250 DM ein, so zahlt der Vertreter noch 325 - 250 = 75 DM, gehen aber Aufträge im Wert von 750 DM ein, so beträgt sein Honorar 750 - 325 = 425 DM.'
Jetzt steht der Vertreter vor folgendem Entscheidungsproblem:
a) Er lehnt ab und versucht, seinen Minimalnutzen VM = 100 durch eine andere Arbeit zu bekommen.
b) Er nimmt den Vertrag an und arbeitet mit geringer Intensität. Sein erwarteter Nutzen (=erwartete Prämie abzüglich Arbeitsintensität) beträgt:
c) Er nimmt den Vertrag an und arbeitet mit hoher Intensität. Dann beträgt sein erwarteter Nutzen:
Arbeitet der Vertreter mit geringer Intensität, so wird sein erwarteter Nutzen negativ. Zwischen der ersten und der dritten Möglichkeit ist er indifferent. Wird der Vertrag geringfügig zu seinen Gunsten modifiziert, wird er ihn annehmen.
Entscheidend ist, daß er aus eigenem Interesse mit hoher Intensität arbeiten wird, denn nur eine hohe Arbeitsintensität garantiert ihm einen positiven Nutzen. Überwachung oder Kontrolle durch die Unternehmung ist nicht nötig; die Unternehmung erhält mit Sicherheit den maximal möglichen Netto-Gewinn von 325 DM. Die Unternehmung trägt also kein Risiko mehr.
Da der Gewinn der Unternehmung unabhängig von der Arbeitsintensität des Vertreters gesichert ist, ist dieses System einer Bezahlung über Umsatzprovisionen deutlich überlegen.
Tabelle 4: Zusammenfassung des Beispiels
Arrow (1963), Uncertainty and the welfare economics of medical care. American Economic Review S. 941-973.
Franke (1982), Grundlagen wirtschaftlichen Verhaltens bei Unsicherheit. WiSt Heft 1, S. 15-20.
Karmann (1992), Principal-Agent-Modelle und Risikoallokation. WiSt Heft 11, S. 557-563.
Kreps (1990), Microeconomics.
Lambsdorff (1994), Adverse Selection und Moral Hazard. WISU, S. 193-194
Mansfield (1994), Applied Microeconomics.
Milde (1988), Die Theorie der adversen Selektion. WiSt Heft 1, S. 1-6
Nell (1993), Versicherungsinduzierte Verhaltensänderungen von Versicherungsnehmern. Karlsruhe.
Ruhl (1989), Erfolgsabhängige Anreizsysteme in ein- und zweistufigen Hierarchien. Heidelberg.
Scherer (1994), Adverse Selection auf Versicherungsmärkten. WiSt Heft 4, S. 201-205.
Schneider (1982), Moral Hazard. WiSt Heft 3, S. 119-120.
Schumann (1992), Grundzüge der mikroökonomischen Theorie. Berlin-Heidelberg-New York.
Thiele (1994), Neue Institutionenökonomik. WISU, S. 993-997
| Referate über:
|
|
Datenschutz |
| Copyright ©
2024 - Alle Rechte vorbehalten AZreferate.com |
Verwenden sie diese referate ihre eigene arbeit zu schaffen. Kopieren oder herunterladen nicht einfach diese # Hauptseite # Kontact / Impressum |
