Referat Kondensator im Wechselstromkreis - Resonanz
Kondensator im Wechselstromkreis
Stromstärke
im C-Kreis
Gesamtspannung : U(t) = U 1 (t) + U C (t)
= I(t)*R ; mit R = 0 Ω & U C (t) = -Q(t)/C :
Q(t)/C =
U 1 (t) : I(t) = 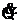 (t) = C*U.1 (t) ; mit U 1
(t) = Û sin(wt) :
(t) = C*U.1 (t) ; mit U 1
(t) = Û sin(wt) :
I(t) = C*Û *w* cos(wt) . Def.: Kapazitive Widerstand X C
= Û/ i
= Û/(C*Û *w) = 1/(w* C) Bem.1.: bei sin-förmigen U : I eff = i /√2
,
analog U
eff : X C = U eff /I eff = 1/(w* C) . 2.: X C ist Blindwiderstand
: keine W el in innere W umgewandelt .
Der R-C-Kreis
Scheinwiderstand
Z = √(R² + X C ²) = Û 1 / i ;
tan φ
= Û C /Û R = X C /R = 1/(w* C* R) (φ hier
neg.) . Û C hinkt I(t) um 90° hinterher
Der R-C-L-Kreis
Z =
Û/ i = √(R² + (X L - X C)²) = √(R² + (w* L -
1/(w*C))².
Resonanz
Bei
best. f 0 (bzw. w 0) : I(t) wird max. : Resonanz(-f) :
Bedingungen(äquivalent zueinander :
wenn 1 vorliegt , liegen auch die anderen vor) : I max. ; φ
= 0 ; Z min. , d.h. Z = R ; Û
R = Û ; Û L = Û C ; Û
L & Û C max. ;
X L = X C : w 0
*L = 1/(w 0 *C) : w 0 = √(1/(L*C)) : f 0 = √(1/(L*C))*1/(2p) .
Leistung im Wechselstromkreis
X L
, C : U(t) = Û sin(wt) ; I(t) = (-) i cos(wt)
R : U(t)
= Û sin(wt) ; I(t) = i sin(wt)
P(t) =
U(t)*I(t) : Momentanleistung
a)
R
: P(t) = I²(t)*R ≥ 0 W
b)
X
C : P(t) = - Û sin(wt)* i cos(wt) : Laden : P(t) > 0 W ; Entladen :
P(t) < 0 W : C liefert W an die Quelle : In 1 Periode ist Gesamtleistung = 0
W .
c)
X
L : Analog zu b) (ohne - ; W el wird W mag wird W
el ) .
Def.: 1.) mittlere Leistung P‾
heißt Wirkleistung (W der Quelle pro Sekunde) .
2.) ohne R : P‾ = 0 W ; der
dabei fließende Strom ist ein Blindstrom .
Wirkleistung bei einer Siebkette
R-C-L-Glied
U(t) = Û
sin(wt) = Û sin(α) ; I(t) = i sin(wt - φ) = i sin(β) ; P(t) = Û *
i sin(wt)sin(wt - φ) (P(t) über Zeit integrieren liefert W)
Einschub
: sin α
*sin β = ½ (cos(α - β) - cos(α + β))
Ferner gilt : Û * i
= √(2) *U eff *√(2) *I eff = 2*U eff
*I eff :
P(t) = 2*U eff *I eff
*½(cos φ -
cos(2wt - φ)) = U
eff *I eff *cos φ .
cos(2wt
- φ) hebt sich über 1 Periode gemittelt auf , cos φ heißt
Leistungsfaktor .
Zeigerdiagramm
:
Transformatoren
Unbelasteter Trafo: Belasteter
Trafo :
Der
ideale Trafo
Def.: idealer Trafo : R der
Primärspule (PS) = 0 Ω , von PS erzeigte Fluss Φ durchsetzt
Sekundärspule (SS) vollständig (gut geschlossene Eisenkerne) .
Der unbelastete Trafo
Primärseite : Sekundärseite
:
R 1 = 0 Ω : I Prim
= Blindstrom , U 1 Induktionsgesetz
: Durch Flussänderung
& I Prim sind 90°
phasenverschoben . Φ.
: wird in SS U 2 (t) = -n 2 *Φ.(t)
Verbraucht im Leerlauf keine W . induziert . Da
Trafo unbelastet : fließt
X L sehr gr. : I Prim
sehr kl. kein
Strom im Sekundärkreis : Fluß Φ
Durch Selbstinduktion : wird
nicht verändert .
U ind (t) = -n 1*Φ.(t)
= - U 1(t) .
Gleichsetzen der Flussänderung :
U 2 (t)/U 1(t) = -n
2 /n 1 = - ü , für Effektivwerte : U 2 , eff /U
1, eff = n 2 /n 1 = ü
Der belastete Trafo
An SS
Wirkwiderstand R legen : Wirkstrom I 2 = U 2 /R :
entnommenes P‾ stammt von PS (EES) : dort zusätzlich zum Blindstrom I
1, blind (mit Φ = 90°) ein Wirkstrom I 1 (mit Φ =
0°) : P‾ = I 2 , eff *U 2 , eff = I 1, eff
*U 1, eff :
I 2 , eff /I
1, eff = U 1, eff /U 2 , eff = n 1/n
2 = 1/ü .
Bem.: Wegen I 1, blind ist I
1, ges > ü* I 2 (Bei guten Trafos : I 1, blind ≈ 0A , da
X L groß ; bei
realen Trafos , wegen
R Prim ≠ 0 Ω
, noch sehr kl. Wirkstrom in PS : verfälscht obere Gleichung) .
Erg.: Spannungen : U 2 , eff
/U 1, eff = n 2 /n 1 = ü (U 2 richtet sich nach U 1)
;
Wirkströme
: I 2 , eff /I 1, eff = n 1 /n 2 =
1/ü (I 1 richtet sich nach
I 2)
Anwendungen
: n 2
<<n 1 , sehr kl. R Sek : sehr hoher I 2
: Schweißtrafo ;
n 2
>>n 1 : U 2 >>U 1 :
Hochspannungstrafo (U
wegen auftretender Leistung lebensgefährlich) .
Bei
Eisenkernen aus einem Stück : Vergrößerung I 1 : es treten
Wirbelströme auf , die Energie aufnehmen : Trafokerne aus Eisenplättchen
aufgebaut , die gegeneinander isoliert sind .
Andere
Erklärung : a)
unbelasteter Trafo : U 1 (t) = Û 1 sin(wt) :
PS : I 1
(t) = i 1, blind cos(wt) (Blindstrom) : verursacht Fluss :
SS : U 2 (t) = - Û 2
sin(wt) , I 2 = 0 A .
b)
belasteter Trafo : SS + R : SS : U 2 (t) = - Û 2 sin(wt)
, I 2 , w (t) = -i 2 , w sin(wt) (Wirkstrom) :
zusätzlicher Fluss : U 1, ind (t) = -Û ind cos(wt) :
I 1, w (t) = i 1, w sin(wt) .
Wirkleistung : P‾ = Û 1 *
i 1 cos φ
bzw. P‾ = Û 1 * i 1,
w :
Wirkströme : i 2 , w / i 1, w = Û 1 /Û 2
= n 1 /n 2
Zeigerdiagramm
der PS :
Transport
elektrischer Energie
Überlandleitungen
sind Hochspannungen :

Reihenschaltung von Lampe
(R = 100 Ω) & R = 1 kΩ (R der Leitungen) : An Leitungen fällt
daher Großteil (90%) der Spannung ab : 90% der el. W bzw. Leistung in Leitungen
verbraten : W / P , die an Lampe abfällt reicht nicht mehr um sie zum Brennen
zu bringen .
Energietransport
mit Hochspannungs- Hochstromtrafos :
T Lampe brennt
Erklärung
: P Lampe
= 0,16 W entnommen aus Trafos , über Leitungen transportiert. Dort auf U = 120
V hochtransformiert : nur Stromstärke von I = P/U = 0,0013 A nötig .
Dieses I
bewirkt , dass in Zuleitungen nur geringe Spannung abfällt :
P Leitung = R*I² = 0,0018 W wird in Leitungen
verbraten , ca. 1% der Leistung (s.o.).
Bem.: P = U*I = R*I² = U²/R , obige
Daten einsetzen : P = 19,6 W falsch :
Schaltung
besteht aus R und X L der Trafos : R = U/I gilt nicht , ist vielmehr
Reihenschaltung : dort für Spannungsabfall an Widerständen : U = R*I .
Differentialgleichungen
Bsp.:
Harmonische mechanische Schwingung
Lin.
Kraftgesetz : F = -D*s (allg.: F res = F = m*a)
Beschleunigung
: a(t) = F(t)/m = -s(t)*D/m , mit a = 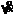 & v =
& v = 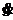 : a =
: a = 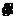 :
:
s(t) =
-s(t)*D/m = -k*s(t) , k = D/m (DGL einer Funktion) .
Lsg.
der DGL :
Lsg.ansatz
raten : s(t) = ŝ sin(wt + φ) : 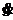 (t) = ŝ* w* cos(wt + φ) : (t) =
(t) = ŝ* w* cos(wt + φ) : (t) =
-ŝ
*w² sin(wt + φ) = -w² * s(t) ;
Vergleich mit DGL : w = √ k = √(D/m) : Für harm. Schwinger mit
Richtgröße D & Masse m gibt es also ∞-viele
Lsgfunktionen
(ŝ , φ unbestimmt) : Bei konkreten Schwing. Anfangsbed. (s(0s) ;
v(0s)) bekannt können ŝ & φ bestimmt werden .
Bsp.
ungedämpftes Pendel
3.)
Anfangsbed. : 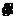 (t) = -w² *s(t) ; w = √(g/L)
= 3,13 1/s , ŝ = 5 cm ,
(t) = -w² *s(t) ; w = √(g/L)
= 3,13 1/s , ŝ = 5 cm ,
s(0s) = 3 cm : s(0s) = 3 cm = 5 cm*sin(3,13*0s + φ ) :
sin(φ
Lsgfunktion
: s(t) = 5 cm * sin(3,13 Hz * t + 0,64) : Winkel im Bogenmaß , da 3,13 Hz auch im
"Rad" .
Elektromagnetische Schwingungen
In diesem Schwingkreis wird W el (t) = ½ CU²(t)
in W mag (t) = ½ L*I²(t) umgewandelt &
umgekehrt
. I(t) & U(t) haben Phasenwinkel von 90°. In R wird Teil der W in innere W
umgewandelt : Schwingung gedämpft .
DGL
der ungedämpften el.mag. Schwingung (R = 0 Ω)
Selbstinduktionsspannung
: U L (t) = -L* 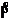 (t) = U C (t) = Q(t)/C : -L*
(t) = U C (t) = Q(t)/C : -L*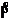 (t) = Q(t)/C
(t) = Q(t)/C
mit I(t)
= 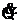 (t) : -L*
(t) : -L*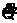 (t) = Q(t)*1/C :
(t) = Q(t)*1/C : 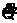 (t) = -Q(t)*1/(L*C)
DGL .
(t) = -Q(t)*1/(L*C)
DGL .
Thomsonsche
Schwingungsgleichung
T = 2p (L*C) . Standard Anfangsbed.: t
0 = 0s : C max. geladen :
Q C
(t 0) =  , Q C (t 0)
=
, Q C (t 0)
=  sin(wt 0 +
φ 0) =
sin(wt 0 +
φ 0) =  : sin φ 0
= 1 : φ 0 = p/2 . Erg.: Q(t) =
: sin φ 0
= 1 : φ 0 = p/2 . Erg.: Q(t) =  cos(wt) =
cos(wt) =  sin(wt + p/2) Ladung auf C ;
sin(wt + p/2) Ladung auf C ;
U(t) =
Q(t)/C = cos(wt)*  /C = Û cos(wt) Spannung am C ;
/C = Û cos(wt) Spannung am C ;
I(t) =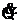 (t) = -
(t) = - *w* sin (wt); i =
*w* sin (wt); i = *w = Û *C/√(L*C) = Û *√(C/L) .
*w = Û *C/√(L*C) = Û *√(C/L) .

