Ähnliche Berichte: Lenzsches Gesetz - Eigeninduktivität einer schlanken Spule [physik] Wärmekraftmaschinen / Dampfmaschinen [physik] Supraleitung - Was ist Supraleitung? [physik] Der Airbag - Das Anti - Blockier - System [physik] Die ökologische Valenz (=Praeferenzbereich) [physik] Solarenergienutzung im Haushalt durch Photovoltaik [physik] Protokoll - Benötigte Geräte, Experimentieranordnung/Versuchsaufbau [physik] Die Atombombe (Technik + Geschichte) [physik]

Projekte: Das dramatische Werk Gerhart Hauptmanns Die Zeit vor 1914 - Das Ende der Monarchie Grundlagen Telekommunikation - Eingangs- und Ausgangsspannung am Koaxialkabel Spezielle Hardware für Digitale Filter - Filter mit 'diskreter' Logik Photovoltaik - Prinzipieller Aufbau und Funktionsweise photovoltaischer

Papers in anderen sprachen: Englisch analyse Franzosisch referate Italienisch hausarbeiten Spanisch seminararbeiten Latein schularbeiten

Referat Lenzsches Gesetz - Eigeninduktivität einer schlanken Spule

physik referate

  Lenzsches Gesetz bei Flussdichteänderung

a) Einschaltvorgang

b) Ausschaltvorgang

a)      Stromkreis geschlossen : I steigt kurzzeitig stark an : 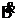>0 T/s ist sehr groß : Aluring fliegt weg : In ihm wird U _ind induziert : I in Ring : erzeugt B-Feld : ist entgegengesetzt zu B-Feld in Eisenkern : Abstoßung : Induziertes B-Feld so gerichtet , dass das anwachsende B-Feld der Spule geschwächt wird . Erklärung : s.o.

b)      Beim Ausschalten : I & B nehmen stark ab : 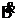< 0 T/s ist sehr groß : Aluring wird angezogen : In ihm wird U _ind induziert : I in Ring : erzeugt B-Feld : ist gleichgerichtet zu B-Feld in Eisenkern : Anziehung : U _ind so gepolt , dass I _ind B-Feld erzeugt , dass das abnehmende B-Feld aufrecht erhalten will . Erklärung : s.o.

Flussänderung durch Anderung der Permeabilitätszahl μ ₀

Eisenstück in stromdurchflossener Spule : B nimmt zu , Stromstärke durch Spule während des Einführens kleiner. Erklärung : Spule selbst ist auch Induktionsspule : In ihr wird U so induziert , dass I _ind der Zunahme von B entgegen wirkt : B-Feld der Spule allein wird kleiner : damit auch I : I = U/R = (U ₀ + U _ind)/R = (U ₀ - n* Φ^.)/R .

Beim Herausziehen ist Φ^.< 0 (da 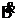< 0) : U _ind pos. (bzgl. U ₀) : I steigt ;

Beim Einführen ist Φ^. > 0 (da 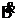 > 0) : U _ind neg. (bzgl. U ₀) : I fällt .

Endgültige Formulierung des Induktionsgesetzes

U _ind = - n*Φ^. ( n von Induktionsspule) .

Selbstinduktion

Hinkender Strom

Selbstinduktion

Unterschied Induktion - Selbstinduktion :

Induktion : Spule induziert U _ind in anderer Spule .

Selbstinduktion : Spule induziert U _ind in sich selbst .

Eigeninduktivität einer schlanken Spule

U _ind = -n*Φ^.

Φ = B*A = μ _r *I* A* n/l : U _ind = -n* μ _r * 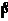*A* n/l 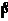= -L* ; L = _r *n² *A/l .

Allg.: L = -U _ind / 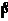 heißt Eigeninduktivität . Abweichungen durch nicht ideal schlanke Spulen : nicht homogen .

Einschaltvorgang

Einschalten : I(t) = U(t)/R = (U ₁ + U _ind)/R = (U ₁ - L*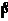(t))/R  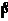: (t) = -(R*I(t)-U ₁)/L =(U ₁ - R*I(t))/L ; t ₀ =0s : 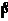(0s) =(U ₁ - R*I(0s))/L =U ₁ /L : |U _ind | = L*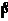(0s)= U ₁.

Im 1. Augenblick ist U _ind = U ₁ .

Induktivität einer belieb. Spule

Gemäß L = U ₁ /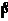(0s) läßt sich die Induktivität aus dem Schaubild des Einschaltvorgangs (s.o.) bestimmen . 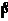(0s) ist die Steigung der Kurve I(t) zum Zeitpunkt t ₀ = 0s . Den ohmschen Widerstand erhält man aus der Asymptote der  I(∞) , dort 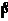(∞)= 0 A/s. I(∞) = U ₁ /R : R = U ₁ /I(∞) .

Ausschaltvorgang

U ₁ = 0 V . : I(t) = U/R = (U ₁ + U _ind)/R = -L* 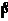/R

Energie des Magnetfeldes

P = U(t)*I(t) = U _ind (t)*I(t) = -L* 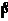(t)*I(t). Bei kl. Zeitraum dt wird dW = P(t)*dt umgewandelt : W = ₀∫ P(t) dt = ₀∫ I(t)* 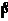(t) dt   [Substitution] = -L _{I 1}∫⁰ I dI

= -L [½ I²]_{I 1} ⁰ = ½ L*I ₁ ²

I ₁ = U ₁ /R ist ursprüngl. Stromstärke vor Ausschalten .

Wechselspannung / -strom

Rotierende Spule (s. Leiterschleife) in B-Feld : U _ind = -n*Φ^. ; Φ(t) = B*A _s (t)

= B* A* cos(wt) = B* A* cos(α(t))  (α = wt heißt Phasenwinkel) :

U _ind = (-)n* B* A* w*(-)sin(t) = n* B* A* w* sin(wt) = Û sin(wt) .

Rotierender Zeiger : Bei Projektion : U(t)

Zeigerdiagramm

Ohmscher Widerstand im Wechselstromkreis

Versuch :

Wenn f der Wechselspannung U genügend hoch : Lämpchen leuchtet konst. hell . Dafür Scheitelwert von Û = 15 V nötig . Bei Gleichspannung benötigt gleich hell leuchtendes Lämpchen Gleichspannung U ₌ = 10 V .

Def. : Der Effektivwert einer U gibt diejenige U ₌ an , die nötig ist , um beim selben R die gleiche mittlere Leistung hervorzubringen : U _eff , analog : I _eff .

Effektivwerte sin-förmiger Wechselspannungen

Bei R = U/I : Momentanleistung : P(t) = U(t)*I(t) = U²(t)*1/R = I²(t)*R , mit

U(t) = Û sin(wt) : P(t) = Û ² sin ²(wt)*1/R = ½ (1 - cos(2wt))*Û ²/R .

Um P zu erhalten : P = ΔW/Δt : ΔW = _0s∫^t ₁ P(t) dt

= (t ₁ - (1/(2w)) sin(2wt ₁))*Û ²/(2R)   ;

Δt = t ₁ - 0s : P = Û ²/(2R) - Û ² sin(2wt ₁) / (4w*R*t ₁) ;

t ₁ ^-> ∞ : P = Û ²/(2R) = U² _eff /R (s.o.) : U _eff = Û / √2 .

Spule im Wechselstromkreis

> (resultierender) Strom I(t) hinkt der angelegten U hinterher .

Herleitung der Stromstärke im L-Kreis

I in Spule : I(t) =(U ₁ (t)+ U _ind (t))/R =(U ₁ (t) - L* 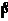(t))/R : R*I(t)= U ₁ (t) - L* 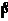(t) . Annahme : R = 0 Ω : L*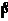(t) = U ₁ (t) bzw. 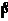(t) = U ₁ (t)/L : I(t) = ∫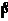(t)dt = ∫U ₁ (t)/L dt     = Û/L ∫ sin(wt) dt = - cos (wt)*Û/(L* w) + c ( c = Gleich-/ Grundstrom) .

Erg.: I(t) ~ -cos(wt) = sin(wt - 90°) : I hinkt angelegtem U um 90° hinterher (bei R = 0 Ω) . Bem.: c ist immer 0 A sobald R nicht exakt 0 Ω .

Def.: induktiver Blindwiderstand X _L = Û/ i = Û/(Û/w* L) = w* L .

Blind- und Wirkwiderstand zugleich : L-R-Kreis

X _L & R in Reihe geschaltete Widerstände : I(t) ist überall gleich . Spannungsabfall am R : U _R (t) = R*I(t) ; Spannungsabfall am X _L : U _L (t) = X _L*I(t) . U _R ist in Phase mit I(t) ; U _L eilt I(t) um 90° voraus .

Zeigerdiagramm :

Beim Drehen : Û erreicht vor i Max. : hinterherhinken bedeutet : die entsprechende Kurve liegt weiter re. (wenn U _R groß : U _L klein) .

Û ² = Û ² _L + Û ² _R = R²I² + (w* L)² I² : Û = i *√(R² + (w* L)²) Gesamt- / Scheinwiderstand : Z = √(R² + X _L²)

φ zwischen angelegtem U & I : tanφ = Û _L /Û _R = X _L /R = w* L/R .

Ist U(t) = Û sin(wt) so fließt I(t) = i sin(wt - φ) .