Referat Physik Spezialgebiet - Die Kernfusion
Physik
Spezialgebiet - Die Kernfusion
1.
Allgemeines zur Kernfusion
1.1 Geschichte der Kernfusion (Fusionsforschung)
1.2 Bedeutung der Kernfusion
2. Die
"natürliche" Kernfusion in der Sonne
2.1 Bethe-Weizsäcker-Zyklus
2.2 Der Proton-Proton Zyklus
3.
Fusionsversuche auf der Erde
3.1 Das Lawson-Kriterium
3.2 Das Prinzip des magnetischen
Einschlusses
3.3 Das Prinzip der Trägheitsfusion
4.
Kernfusionsreaktionen
4.1 Deuterium-Tritium Fusion
1.
Die Kernfusion
Bei der
Kernfusion, wie man sie für die Energiegewinnung nutzen will, verschmelzen zwei
leichtere Kerne zu einem schwereren. Dabei ist das gemeinsame Gewicht der zwei
leichteren Kerne immer noch größer als das des schwereren Kerns. Die "fehlende"
Masse wurde bei dieser Reaktion direkt in Energie umgewandelt. (Massendefekt)
Diese Energie wird in Form von Hitze frei - die Reaktion ist folglich eine
stark exotherme Reaktion.
Atomkerne
sind positiv geladen, stoßen sich also gegenseitig ab. Diese elektrische Kraft,
welche bei weitem größer als die Gravitationskraft ist, nennt sich
"Coulomb-Kraft". Sie verstärkt sich je näher die beiden Atomkerne zueinander
kommen. Sollten sich die Atomkerne aber nahe genug gekommen sein, so wird eine
anziehende Kraft wirksam, welche die Fusion der beiden Kerne erlaubt. Diese
Annäherung ist aber nur möglich, wenn die Atomkerne eine genügend hohe
Geschwindigkeit besitzen. In einem Gas oder Plasma bewegen sich die Atome
unabhängig von einander - es ist also nur der Durchschnitt aller
Geschwindigkeiten von Relevanz. Haben die Teilchen im Mittel eine hohe
Geschwindigkeit, so spricht man von einer hohen Temperatur (Kelvin) oder hoher
Bewegungsenergie (angegeben in Elektronenvolt eV). Die für die Fusion benötigte
Geschwindigkeit wird nur in Teilchenbeschleunigern oder in Plasma mit einer
sehr hohen Temperatur erreicht.
Der
Atomkern selbst besteht aus positiv geladenen Protonen und neutral geladenen
Neutronen - die so genannten Nukleonen. Die Masse eines Atomkerns ist im
Allgemeinen kleiner als die Masse seiner Nukleonen (Kernteilchen). Diese
Massendifferenz m wird nach Einsteins Formel (E = mc²) bei der Entstehung eines
Atomkerns aus Nukleonen in Form von kinetischer Energie oder als eine
elektromagnetische Welle freigesetzt.
Leichtere
Elemente, wie Wasserstoff, oder schwerere Elemente, wie z.B. Uran, haben
geringere Bindungsenergien pro Nukleon. Daher wird bei der Spaltung von
schweren Elementen, wobei leichtere Kerne entstehen, Energie frei (Kernfission/
Kernspaltung).
Bei der
Fusion (Verschmelzung) von leichten Atomkernen erhält man ebenfalls Energie.
In
dieser Grafik ist die Kernbindungsenergie pro Nukleon aufgezeichnet. Es ist zu
erkennen, dass die Nukleonen der leichteren Kerne weniger stark gebunden sind
als die der verhältnismäßig schwereren bis zum Eisen. Eisen stellt das
stabilste Element im Periodensystem dar. Je näher die Elemente am Kurvenmaximum
(beim Eisen) liegen, desto mehr Energie wird bei ihrer Entstehung frei.
Der
Energieoutput durch Fusion bzw. Fission lässt sich aus dieser Grafik insofern
abschätzen, als dass man die Differenz der Kernbindungsenergien betrachtet.
1.1
Allgemeines zur Kernfusion
Die Sonne, die uns seit einigen Milliarden Jahren
gleichmäßig und problemlos mit Energie versorgt, macht das Leben auf unserem
Planeten erst möglich. Sie ist für uns geradezu ein Symbol einer sicheren und
im Einklang mit der Natur stehenden Energiequelle. Die grundlegenden Prozesse,
aus denen unsere Sonne und alle Sterne, die wir am nächtlichen Himmel sehen,
ihre Energie beziehen, sind Reaktionen, bei denen Wasserstoff zu Helium
'verbrannt' wird. Dabei werden die Bindungskräfte zwischen den
Bausteinen der Atomkerne freigesetzt. Seit langem ist es Ziel intensiver
Grundlagenforschung die Details der Wechselwirkungskräfte zu entschlüsseln, die
darin enthaltenen Energien zu kontrollieren und für die Energieerzeugung in
Kraftwerken nutzbar zu machen. Dies ist ein weiter Weg, aber die physikalische
Grundlagenforschung hat bereits die ersten Schritte auf diesem Weg getan. Das
Hauptproblem ist, den Brennstoff auf extrem hohe Temperaturen aufzuheizen und
lange genug zusammenzuhalten. Die Sonne löst diese Aufgabe durch die gewaltigen
Gravitationskräfte ihrer riesigen Masse. Der erste Ansatz, dieses Problem auf
der Erde zu lösen bestand darin, den Fusionsbrennstoff durch starke Magnetfelder,
von den Gefäßwänden isoliert, zusammenzuhalten. (siehe Prinzip des magnetischen
Einschlusses)
Ein alternativer Ansatz nutzt die den
Gravitationskräften verwandten Trägheitskräfte, während der Fusionsbrennstoff
etwa 1000fach verdichtet, aufgeheizt und
schließlich gezündet wird. Mit Hilfe intensiver Laserstrahlen und
Schwerionenstrahlen erscheint es heute aussichtsreich, dieses Konzept zunächst
im Laborbereich und später in einem Kraftwerkskonzept umzusetzen.
Geschichte
der Kernfusion
Die Idee,
das Sonnenfeuer auf der Erde zu zünden und kontrolliert als nahezu
unerschöpfliche, sichere und relativ saubere Energiequelle zu nutzen, ist nun
schon mehr als 50 Jahre alt. Doch die Umsetzung hat sich als sehr viel
schwieriger und kostspieliger erwiesen als einst angenommen. Immer weniger
Regierungen (und damit die wichtigsten Geldgeber) sind bereit die horrenden
Summen für die Entwicklung dieser Technologie aufzuwenden, welche
voraussichtlich nicht vor Mitte des nächsten Jahrhunderts, wenn überhaupt, praktisch
einsetzbar sein wird.
Nach
etlichen europäischen Projekten wie dem Joint European Torus (JET) - bei diesem
Projekt wurde eine Rekord-Energieausbeute von 60% erzielt - einigten sich vor
15 Jahren Europa, Japan, die ehemalige Sowjetunion und die USA auf den eines
Internationalen Thermonuklearen Experimental-Reaktors. (ITER) Dieser sollte die
Machbarkeit eines technischen Fusionskraftwerks demonstrieren und erstmals
genauso viel Energie liefern wie für die Zündung benötigt wird. Doch aufgrund
der enormen Kosten von über 7 Milliarden Euro für den Bau und weiteren 400.000
Euro an jährlichen Betriebskosten beschloss der ITER-Rat die Realisierung um 3
Jahre zu verschieben. Nun wird es wohl nur noch eine abgemagerte, halb so teure
Version geben, die wichtige technische und physikalische Fragen klären soll,
nicht aber eine positive Gesamtenergiebilanz erreichen wird.
Bedeutung
der Kernfusion
Die
Triebfeder für die Forschung war und ist das Wissen, dass aus einem Fingerhut
voll flüssigem schwerem Wasserstoff gleich viel Energie gewonnen werden könnte
wie aus 20 Tonnen Kohle. Wir leben in einer Zeit, in der, der Grossteil des
Weltenergiebedarfs durch fossile Energieträger, wie Erdöl, Erdgas und Kohle
gedeckt wird. Die Zeit, in der diese Vorkommen erschöpft sein werden, rückt
jedoch mit Riesenschritten näher. Experten rechnen damit, dass innerhalb der
nächsten 50 Jahre diese Ressourcen aufgebraucht sein werden. Doch wie wird dann
der stetig steigende Energiebedarf der Weltbevölkerung zu stillen sein?
Bis vor
kurzem sah man die Energiegewinnung aus der Kernspaltung als das
Zukunftsmodell. Doch spätestens nach Tschernobyl im Jahre 1986 wurden die
Mängel dieser Energiegewinnung deutlich. Es sind aber nicht alleine
Sicherheitsrisiken, die diese Methode fragwürdig erscheinen lassen. Der
amerikanische Physiker R. F. Post hat durch Berechnungen herausgefunden, dass
in einem AKW mit einer Leistung von 1000 MW pro Woche langlebige radioaktive
Spaltprodukte mit einer Gesamtaktivität von 20 Atombomben des Typs, der auch
über Hiroshima abgeworfen worden war, frei würden. Würde man also den gesamten
Energiebedarf der USA durch Kernkraftwerke stillen, entstünde wöchentlich mehr
Radioaktivität als bei 5000 Atombomben.
Neben
eher unbekannten Formen der Energiegewinnung, wie zum Beispiel
Biomasseverbrennung, wird die Wind-, Wasser- und Sonnenenergie als die
"sauberste" Methode der Energiegewinnung gesehen. Doch der Traum vieler
Wissenschaftler ist seit Mitte des 20. Jahrhunderts die Energiegewinnung
durch Kernfusion.
Die Vorteile
liegen auf der Hand. Neben einem gewaltigen Energiepotential punktet diese
Technologie durch verschwindend geringe Strahlenbelastung im Gegensatz zur
Kernspaltung und der Verwendung des Rohstoffs Wasser, welcher auf der Erde im
Überfluss vorhanden ist.
Bei dem
Fusionsbrennstoff handelt es sich um Deuteriumoxyd - besser bekannt unter der
Bezeichnung "schweres Wasser" - dessen natürlicher Anteil im Wasser 0,02
Prozent beträgt. Auch die Gewinnung ist
verhältnismäßig billig. In einem solchen Kraftwerk könnten in der Zukunft aus
einem Gramm Brennstoff ca. 90 000 kwh erzeugt werden. (= 11t Kohle) Der
Energiegehalt des Deuteriums ist wiederum noch etwa zehnmal größer als der des
spaltbaren Urans (U235). In einem Liter Wasser steckt auf Grund seines Deuterium-Gehalts
genauso viel Energie wie in 300 Liter Benzin. Ein Kubik- Kilometer Meerwasser
würde genügen, um den gegenwärtigen Energiebedarf Europas tausend Jahre lang zu
decken. Selbst wenn der Energiebedarf der Menschheit um das Tausendfache
ansteigen sollte, könnte der Energievorrat, welcher im Deuterium-Gehalt der
Weltmeere schlummert, nicht in 100 000 000 Jahren aufgebraucht werden. Darum
kann man die kontrollierte Kernschmelzung als Endlösung aller
Energieversorgungsprobleme bezeichnen. Wenn sie gelingt, wäre sie fortan und
bis zum Ende eines zivilisierten menschlichen Daseins auf der Erde die
Energiequelle schlechthin.
Abb. 4.1 - Vergleich Menge des Energieträgers -
daraus gewonnene Energie
2.
Die "natürliche" Kernfusion in der Sonne
Ein
gutes Beispiel für einen funktionierenden "Fusionsreaktor" liefert uns die
Sonne selbst. Das für alle Stern so wichtige "Wasserstoffbrennen" kommt nach
Erreichen von einer Temperatur von über 5 Millionen Kelvin in Gang. Neben der
hohen Temperatur ist der enorm hohe Druck von 233 Gigabar (entspricht etwa der
2000fachen Verdichtung von festem Wasserstoff, wie er heutzutage unter
Laborbedingungen erreichbar ist) im Zentrum der Sonne eine Voraussetzung für
die funktionierende Kernschmelze. In der Sonne werden pro Sekunde 600 Millionen
Tonnen Wasserstoff zu 596 Millionen Tonnen Helium "verbrannt". Die fehlenden 4
Tonnen (= 0,66%) werden in Energie umgesetzt. (Massendefekt) Trotz dieses
Massenverlustes hat die Sonne in 4,5 Milliarden Jahren nur 3 Promille ihrer
Gesamtmasse verloren.
Dabei
sind 2 Prozesse von wichtiger Bedeutung:
2.1
Bethe-Weizsäcker-Zyklus (Abb. 5.1):
Dieser
Zyklus wird gelegentlich auch Kohlen-Stickstoff-Zyklus (C-N-Zyklus) genannt, da
diese beiden Elemente in ihm eine Rolle spielen. Beim Zyklusbeginn stößt ein
Kohlenstoffatom vom Atomgewicht 12 mit einem Proton (Wasserstoffkern) zusammen
und vereinigt sich zu einem instabilen Stickstoffisotop mit dem Atomgewicht 13.
Zu Ende dieses Zyklus kommt das am Anfang hineingesteckte Kohlenstoffatom
unverändert wieder heraus. Stickstoff (Atomgewicht 15) und ein Proton teilen
sich auf in eben diese Kohlenstoffatom und ein Heliumatom (Atomgewicht 4).
 Abb. 5.1
Abb. 5.1
Das
Kohlenstoffatom spielt also nur eine Art Katalysator in dieser Reaktion. Die
Energieabgabe geschieht entweder in Form von kinetischer Energie durch die an
zwei Stellen herausfliegenden Neutrinos und Positronen oder vor allem durch
Gammastrahlung. Bei derartigen atomaren Reaktionen (hier Kernschmelze oder
Kernfusion) wird nach der aus der speziellen Relativitätstheorie stammenden
Formel "E = m*c²" Masse in Energie verwandelt. Für die einzelne Verwandlung von
4 Wasserstoffkernen zu einem Heliumkern gilt also folgende Rechnung:
|
Atomkern
|
Atomgewicht
|
|
|
|
|
Wasserstoffkern
|
|
|
Heliumkern
|
|
Bei 4
Wasserstoffkernen, welche zu einem Heliumkern verschmelzen, ergibt sich eine
Differenz von 0,028 Atomgewichtseinheiten (Massendefekt). Diese Differenz ist
direkt in Energie in der Höhe von 25,0 Millionen Elektronenvolt (25 MeV) oder 4
* 10-12 J umgewandelt worden. (1 eV ≈ 1.602 × 10-19
J)
|
C + 1H → 13N
+ γ + 1,95 MeV
|
1,3⋅107 Jahre
|
|
N → 13C + e+
+ νe + 1,37 MeV
|
7 Minuten
|
|
C + 1H → 14N
+ γ + 7,54 MeV
|
2,7⋅106 Jahre
|
|
N + 1H → 15O
+ γ + 7,35 MeV
|
3,2⋅108 Jahre
|
|
O → 15N + e+
+ νe + 1,86 MeV
|
82 Sekunden
|
|
N + 1H → 12C
+ 4He + 4,96 MeV
|
1,12⋅105 Jahre
|
Die
einzelnen Schritte dieses Zyklus dauern verschieden lang - der langsamste ist
im Mittel der Einfang des 3. Protons mit 320 Millionen Jahren. Diese sehr
zeitaufwendigen Schritte machen diesen Zyklus für Laborversuche nutzlos - eine
weitere Voraussetzung, die zwar auf der Sonne gegeben ist, auf der Erde aber
nicht erreicht werden kann. Auf der Sonne laufen diese Schritte nebeneinander,
weshalb eine kontinuierliche und ergiebige Energieerzeugung gewährleistet ist.
2.2
Der Proton-Proton Zyklus(Abb. 7.1)
Bei
diesem Zyklus reagieren zwei Protonen unmittelbar miteinander und bilden einen
Deuteriumkern (1). Dieser regiert mit einem weiteren Proton zu Helium 3 (2).
Zwei dieser Helium-3-Kerne verschmelzen dann zu einem Helium-4-Kern, wobei
wiederum zwei Protonen für weitere Zyklen frei werden (3).
|
|
|
|
|
|
Abb.
7.1
Die
Gesamtenergieabgabe beträgt hier 26 MeV oder 4,2 * 10-12 J.
Welcher
der beiden Zyklen ergiebiger ist, hängt von der jeweiligen Temperatur ab.
3.
Fusionsversuche auf der Erde
Das Hauptproblem der zivilen Kernfusionsforschung sind die
hohen Zündtemperaturen; Die Fusionsprozesse kommen erst bei Temperaturen von
hundert Millionen Grad Celsius in Gang. Diese sind notwendig, um die elektrostatischen
Abwehrkräfte (Coulomb-Abstoßung) zwischen den Atomkernen zu überwinden. Nur bei
geringen Teilchenabständen gelingt es, den Fusionsprozess einzuleiten. Sinn
machen würde der Prozess also nur, wenn in der Reaktion mindestens soviel
Energie freigesetzt würde, wie zum Aufheizen nötig war. Diese Bedingungen
wurden vom englischen Forscher John Lawson zum ersten Mal formuliert. Er gab
an, welche Anforderungen an die Teilchendichte n und die Einschlusszeit t für
den Brennstoff gelten müssen, wenn die Zündtemperatur erst einmal erreicht
wurde.
3.1 Das Lawson Kriterium
Lawson Kriterium: n 1014
s/cm3
Für eine
"erfolgreiche" Kernfusion - also eine produktive Kernfusion - muss also
entweder die Teilchendichte n sehr klein und die Einschlusszeit t groß sein
oder umgekehrt. Derzeit wird in beide Richtungen intensiv geforscht.
|
Methode
|
 (m-3)
(Teilchendichte) (m-3)
(Teilchendichte)
|
 (s) (s)
(Einschlusszeit)
|
|
Magnetischer
Einschluss
|
|
|
|
Trägheitseinschluss
|
|
|
Magnetischer
Einschluss:
die
Teilchendichten sind sehr gering (beinahe Vakuumbedingungen), dann kann die
Einschlusszeit verhältnismäßig groß aus ausfallen (im Bereich von Sekunden).
Trägheitsfusion:
Die
Teilchendichten bewegen sich um 1030 pro m³, während die
Einschlusszeiten nur Millionstel Sekunden ausmachen.
Welche
dieser Forschungen näher am Ziel ist, kann beurteilt werden, wenn das Fusionsprodukt
aus Teilchenzahldichte n, Einschlusszeit t und Temperatur T für beide Methoden
verglichen wird. (Abb 9.1)
Abb.
9.1 - Offene Kreise -
magnetische Einschlussexperimente
Geschlossene
Rechtecke - Trägheitsfusionsexperimente
Man
sieht an dieser Grafik, dass die Erfolge der beiden Forschungsrichtungen mehr
oder weniger parallel verlaufen. Es ist also derzeit noch nicht abzuschätzen
welche sich durchsetzen wird.
Dieses
Diagramm steht insofern mit dem Lawson Kriterium im Zusammenhang, als dass es
ebenfalls Teilchendichte X Einschlusszeit inkludiert. Hinzu kommt die
Temperatur als ein weiterer ausschlaggebender Wertungsfaktor.
3.2
Das Prinzip des magnetischen Einschlusses
Bei Temperaturen von über 100 Millionen Grad würden alle
Materialen, die den Brennstoff einschließen, schmelzen beziehungsweise
verdampfen. Daher wird der Brennstoff bei derzeitigen Versuchen in Plasma -
Form (Atom ist aufgetrennt: Elektronen und Atomkern bewegen sich unabhängig
voneinander) im Vakuum, ohne Berührung mit dem Behälter, gezündet. Er wird
durch starke Magnete, die um die ringförmige Reaktionskammer errichtet werden,
auf der Bahn und mit Abstand zu den Gefäßwänden gehalten. Zusätzlich
müssen die Magnete stark gekühlt werden, sodass sie
überhaupt die benötigte Stärke erreichen.
Diese Methode arbeitet mit sehr kleinen Teilchenzahldichten,
das heißt, dass die Einschlusszeit im Bereich von Sekunden liegen muss, um das
Lawson Kriterium zu erfüllen. Die Teilchenzahldichte liegt bei ca. 1014
/cm³, was ungefähr Vakuumbedingungen entspricht.
Historisch gesehen ist die Methode des magnetischen
Einschlusses die ältere - so genannte Tokamak- und Stellaratoranlagen sind die
erfolgreichsten Maschinen auf diesem Gebiet. In Europa wird fast ausschließlich
das Konzept des magnetischen Einschlusses verfolgt. Bekannte Beispiele sind der
JET- Reaktor (Joint European Torus) in England und der geplante ITER Reaktor.
Die
Probleme dieses Verfahrens liegen auf der Hand: Das Kühlen der Magnete, das
Halten und Erhitzen des Plasmas benötigt enorme Energiemengen, bis der
Fusionsprozess überhaupt einsetzt. Bei bisherigen Projekten konnte die Fusion
nur über kurze Zeit aufrechterhalten werden, so dass die durch die Fusion
gewonnene Energie nur einem kleinen Teil der eingesetzten Energie entsprach.
3.3
Das Prinzip der Trägheitsfusion
Diese
Methode geht von einer sehr hohen Teilchenzahldichte (über 1024 /
cm³) und Einschlusszeiten in der Größenordnung von Nanosekunden aus. Der Ablauf
ist in Abb. 10.1 schematisch dargestellt.
Abb.
10.1
Phase
1:
In
diesem Fall besteht das Fusionstarget aus einer hohlen Plastikkugel (wenige
Millimeter Durchmesser), welche auf der Innenwand eine Schicht mit festem
gefrorenem Wasserstoff aufweist - bestehend aus den schweren Isotopen Deuterium
und Tritium. Das innere ist nicht vollständig evakuiert, sondern mit einem
gasförmigen Deuterium-Gemisch gefüllt.
Phase
2:
Ein
solches Fusionstarget wird nun mit einem intensiven Ionen- beziehungsweise
Laserstrahl schlagartig auf 3 Millionen Grad erhitzt und verwandelt sich in
Folge in heißes Plasma. Hier werden vorzugsweise Laserstrahlen benutzt, da
diese Technologie weiter fortgeschritten ist. Dieses Plasma expandiert nun von
der Oberfläche weg - durch den Rückstoß des expandierenden Plasmas wird der
Rest des Targets stark komprimiert. Dabei wird eine 1000-fache Kompression des
Brennstoffs erreicht, der dabei aber auf eine Temperatur von nur 1 Million
Kelvin aufgeheizt wird. Der gasförmige Anteil wird ebenfalls kugelsymmetrisch
komprimiert.
Phase
3:
Eine
einlaufende Stoßwelle heizt schließlich den zentralen Teil des Targets auf
40-100 Millionen Grad auf. Diese Temperatur ist nun hoch genug, um im
hochkomprimierten, kleinen zentralen Bereich die Zündbedingungen zu erreichen.
Die große Zahl an frei werdenden Alphateilchen und Neutronen erhitzen nun auch
den ebenfalls hochkomprimierten, aber noch wesentlich kälteren Teil, der
außerhalb des zentralen Zündbereichs liegt und zünden ihn damit ebenfalls.
Phase
4:
Eine
Brennfront, die zur Fusion eines großen Teils des Brennstoffs führt, breitet sich
im Target aus.
Die
große Herausforderung bei der Anwendung dieser Methode ist die Erhaltung der
Kugelsymmetrie während des gesamten Vorgangs. Schon eine geringste Veränderung
dieser idealen sphärischen Form von etwas mehr als einem Prozent bewirkt eine
starke Deformation im Verlauf des Kompressionsprozesses und damit wird es
unmöglich die Zündbedingungen zu erreichen. Eine derart symmetrische
Bestrahlung mit Ionen- bzw. Laserstrahlung zu erreichen ist sehr kompliziert.
Deshalb wird in jüngeren Experimenten eine vorherige Aufheizung des
Fusionstargets forciert - das Target wird von allen Seiten gleichmäßig
"geröstet". Die Komprimierung und Zündung erfolgt erst danach.
Diese
Methode wird von amerikanischen Wissenschaftlern viel eher verfolgt, als von ihren
europäischen Kollegen. In Europa wird nach der Methode des magnetischen
Einschlusses geforscht und nur etwa 1% des Gesamtforschungsetats für die
Erforschung der Trägheitsfusion aufgewandt.
4.
Kernfusionsreaktionen
In
dieser Grafik sind einige Kernfusionsreaktionen, bei welchen Wasserstoffisotope
miteinander verschmelzen, deren Ausgangsstoffe, Produkte, Zündungstemperatur
und deren Energieoutput aufgelistet. Diese Reaktionen sind für uns nicht nur
deshalb wichtig, weil sie auf der Sonne von Relevanz sind (siehe
Proton-Proton-Zyklus), sondern auch weil der Rohstoff Wasser auf der Erde
beinahe grenzenlos verfügbar ist und deshalb eine Nutzung für die
Energiegewinnung nahe liegt. Die Erforschung der ersten Reaktion wird von
Wissenschaftlern sehr entschlossen verfolgt; Obwohl sie nicht den größten
Output liefert, sind die Rahmenbedingungen für die Fusion doch weitaus leichter
zu erlangen als bei der Fusion von Deuterium und dem Helium 3 - Isotop.
Einerseits ist es sehr schwer die Zündtemperatur von über 350 Millionen Grad zu
erreichen, andererseits ist der Brennstoff He3 auf der Erde in nur sehr
geringen Mengen vorhanden.
Deshalb
wird in Prototyp-Reaktoren häufig ein Deuterium-Tritium-Gemisch versucht zur
Fusion zu bringen.
4.1
Deuterium-Tritium Fusion
Die wohl
aussichtsreichste Fusionsreaktion ist die Deuterium-Tritium Fusion. Diese
Reaktion läuft folgendermaßen ab:
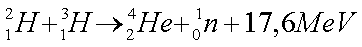
Die
Gewinnung des Fusionstreibstoffs Deuterium sollte keine Probleme bereiten, da
es ca. 1/5000 des natürlichen Wasseranteils ausmacht. Der Fusionstreibstoff
Tritium hingegen wird am besten aus Lithium gebrütet.
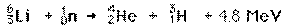
Quellen:
Dtv-Atlas
zur Astronomie
Microsoft
Encarta
https://www.net-lexikon.de
Spektrum
der Wissenschaft, Oktober 1998
Dtv-Atlas
zur Atomphysik
https://hyperphysics.phy-astr.gsu.edu