Referat Protokoll zum Versuch Trägheitsmoment / Drehmoment

Protokoll zum Versuch

Trägheitsmoment / Drehmoment

Aufgabenstellung

A) Untersuchen Sie die Abhängigkeit der Winkelbeschleunigung eines hantelförmigen Körpers vom Betrage einer tangential angreifenden Antriebskraft bei konstantem Radius!

B) Untersuchen Sie die Abhängigkeit der Winkelbeschleunigung eines hantel- förmigen Körpers vom Antriebsradius einer tangential angreifenden Kraft!

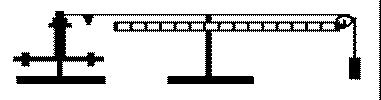
_{Geräte und Hilfsmittel:}

. Hantel mit Zylinder

. 2 Stativstangen mit Füßen

. Trommel mit Schnur

. Meßstab mit Rolle

. 2 Massestücke zu je 100g

. Körper zu 10g, 20g, 50g, 100g

. Stoppuhr

_{Vorbetrachtungen:}

. Leiten Sie aus dem Weg-Zeit-Gesetz und dem Geschwindigkeits-Zeit-Gesetz der gleichmäßig beschleunigten Bewegung für v = 0 und s = 0 eine Gleichung her, mit der Sie aus Gesamtweg s und Gesamtzeit t die Endgeschwindigkeit v errechnen können!

_{I s } ^a _t

²

II v  at

_{a } s _t

a  ^v t

_{I in II}

_{v } ^st _ ^s

_{t t}

. Ein Punkt an der Peripherie eines Rotationskörpers bewegt sich mit der Ge- schwindigkeit v. Wie kann man die Winkelgeschwindigkeit des Körpers berechnen?

Die Winkelgeschwindigkeit des Körpers ist direkt proportional zum Radius r der

Peripherie sowie zur Endbahngeschwindigkeit v, daher gilt

_ ^v _.

^r

. Wie errechnet man ein Drehmoment M? Sind in der Experimentieranordnung die

Richtungsbedingungen erfüllt?

M_D = Fr

Das Drehmoment ist ein Vektor; es stellt ein Maß für die Drehwirkung einer an einem drehbaren starren Körper angreifende Kraft dar. Der Betrag M des Drehmomentes ist dabei gleich dem Produkt aus dem Betrag F der angreifenden Kraft und dem senkrechten Abstand r ihrer Wirkungslinie vom Drehpunkt:

Da in diesem Fall die Kraft F senkrecht zum Abstand ihrer Wirkungslinie vom

Drehpunkt (tangential) angreift ist die Richtungsbedingung erfüllt.

_Auswertung:

. Berechnen Sie für jede Antriebskraft F bzw. für jeden Antriebsradius r die Endbahngeschwindigkeit v, die Endwinkelgeschwindigkeit  und die Winkelbeschleunigung !

siehe Tabelle

. Stellen Sie in Abhängigkeit von F bzw. r grafisch dar! Welche

Gesetzmäßigkeiten erkennen Sie aus den Darstellungen?

siehe Diagramme 1 & 2

In Diagramm 1 und 2 wird jeweils die Abhängigkeit der Winkelbeschleunigung  von der Antriebskraft F bzw. -radius r dargestellt. Alle gezeigten Graphen scheinen einen linearen Verlauf zu beschreiben, was auf direkte Proportionalität zwischen den jeweiligen Größen schließen läßt.

~ F

_

_{~ r}

~ Fr



. Berechnen Sie für alle Antriebskräfte F und für alle Antriebsradien r das Dreh- moment M_D Fr, und stellen Sie die gemessene Winkelbeschleunigung in Abhängigkeit vom Drehmoment grafisch dar! Welcher gesetzmäßige Zusammen- hang ist aus der Darstellung erkennbar?

siehe Tabelle und Diagramm 3

Der Graph, welcher die Abhängigkeit der Winkelbeschleunigung  vom

Drehmoment M beschreibt, scheint ebenfalls einen linearen Verkauf zu nehmen,

was ebenso auf direkte Proportionalität hinweist.

~ M

Daraus folgt, das der folgende Quotient konstant ist:

^M _{ konstant.}

Dieser Quotient hei t Trägheitsmoment J eines Körpers und ist ein Maß dafür,

_{welchen Widerstand dieser der Anderung seiner Winkelgeschwindigkeit}

entgegensetzt.

. Bestimmen Sie aus dieser letzten Darstellung das Trägheitsmoment der

Experimentierapparatur!

siehe Tabelle

. Bei den Messungen wurde die Reibung vernachlässigt. In welchem Sinne wirkt sich diese Vernachlässigung auf den Betrag des errechneten Trägheitsmomentes aus?

Fehlerbetrachtung:

Da die Reibung bei den Messungen vernachlässigt wurde, ist der Betrag des Trägheitsmomentes J größer, als er eigentlich sein müßte. Die Winkelbeschleunigung  ist maßgebend für das Trägheitsmoment J. Ihr Wert fällt allerdings etwas geringer aus, da während der Beschleunigung Reibungskräfte der Antriebskraft entgegenwirken. Da die Winkelbeschleunigung  bei der Berechnung des Trägheitsmomentes J im Nenner steht, wird der Betrag des gesamten Terms unweigerlich größer.

Anderweitig werden alle gemessen Werte, wie Zeit- und Radienmessung durch den Faktor Mensch mit Fehlern behaftet, was sich negativ auf die Auswertung auswirken kann.

Tabelle

_{Meßwerte für zwei Massestücke zu je 100 g bei 0 m Abstand zur Drehachse}

Diagramme fehlen!