Der elektrische Schwingkreis
Zunächst lautet die allgemeine Definition: Ein
Schwingkreis ist eine Schaltung (ein Kreis) aus einem Kondensator und einer
Spule. Dies lässt sich dadurch begründen, dass in dieser Schaltung elektrische
Schwingungen stattfinden können .
Folglich lassen sich Schwingkreise aus Induktivitäten (Spulen) und Kapazitäten
(Kondensatoren) erstellen, so auch ein Parallelschwingkreis aus dem Kondensator
mit der Kapazität 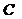 und einer Spule mit der Induktivität L. Es sei gesagt, dass man die Induktivität L einer Spule mit der Länge l,
sowie der Querschnittsfläche A und
der Windungsanzahl n mit Hilfe der Formel
und einer Spule mit der Induktivität L. Es sei gesagt, dass man die Induktivität L einer Spule mit der Länge l,
sowie der Querschnittsfläche A und
der Windungsanzahl n mit Hilfe der Formel  (dabei entspricht
(dabei entspricht  der Permeabilitätszahl
1 und
der Permeabilitätszahl
1 und  der magnetischen
Feldkonstante
der magnetischen
Feldkonstante  .......1,2566370614
.......1,2566370614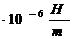 = 4
= 4 )
)
berechnen kann,
wobei die Induktivität L die Einheit  (1 Henry) besitzt .
Wenn man von einem geladenen Kondensator als Bedingung für die Schwingung
ausgeht und den ohmschen Widerstand zunächst vernachlässigt, findet in einem Schwingkreis (s.Abb.1) ein periodischer
Austausch von magnetischer- (Spule) in elektrische Feldenergie (Kondensator)
und umgekehrt statt, denn die Ladungen schwingen zwischen Kondensator und Spule
hin und her und es ereignet sich folgendes: Sobald sich der Kondensator
aufgeladen hat, also elektrische
(1 Henry) besitzt .
Wenn man von einem geladenen Kondensator als Bedingung für die Schwingung
ausgeht und den ohmschen Widerstand zunächst vernachlässigt, findet in einem Schwingkreis (s.Abb.1) ein periodischer
Austausch von magnetischer- (Spule) in elektrische Feldenergie (Kondensator)
und umgekehrt statt, denn die Ladungen schwingen zwischen Kondensator und Spule
hin und her und es ereignet sich folgendes: Sobald sich der Kondensator
aufgeladen hat, also elektrische
|
 Abb. Schaltbild Schwingkreis aus
Kondensator und Spule Abb. Schaltbild Schwingkreis aus
Kondensator und Spule
|
Energie
gespeichert hat, beginnt er sich über die Spule wieder zu entladen. Der
Entladestrom baut wiederum um die Spule ein Magnetfeld auf und damit ist die
elektrische-
wieder in magnetische Feldenergie zurückverwandelt
(genauere Betrachtung s. 2.1.Pasenverschiebung) Dieser periodische Vorgang bewirkt eine sinusförmige
Spannungsschwankung.
|
Durch die relativ hohen Leitungswiderstände (starke
Dämpfung; Wärmeverlust der Bauteile vor allem der Spule) sinkt die Amplitude
allerdings schon nach wenigen Schwingungen wieder auf null ab, d.h. es ist eine
freie gedämpfte magnetische Schwingung vorhanden. Aufgrund verschiedener
Versuche, wie z.B. die Kapazität C
und/oder die Induktivität L zu
variieren, konnte man feststellen, dass jeder Schwingkreis eine bestimmte
Eigenfrequenz f besitzt, die man nach der Thomson'schen Gleichung
 , mit der Induktivität
L und der Kapazität C, berechnen kann. Aus der Thomson'schen Gleichung folgt die
Erkenntnis, dass der Quotient größer wird und somit die Eigenfrequenz
, mit der Induktivität
L und der Kapazität C, berechnen kann. Aus der Thomson'schen Gleichung folgt die
Erkenntnis, dass der Quotient größer wird und somit die Eigenfrequenz  zunimmt, wenn man die
Kapazität C oder die Induktivität L verkleinert. Wird nun der Schwingkreis
durch eine periodische Spannung zum Schwingen angeregt zeigt dieser ein
Resonanzverhalten, das von der Dämpfung (z.B. ohmscher Widerstand) abhängig
ist, wobei die Amplitude der Schwingung (
zunimmt, wenn man die
Kapazität C oder die Induktivität L verkleinert. Wird nun der Schwingkreis
durch eine periodische Spannung zum Schwingen angeregt zeigt dieser ein
Resonanzverhalten, das von der Dämpfung (z.B. ohmscher Widerstand) abhängig
ist, wobei die Amplitude der Schwingung ( bzw.
bzw.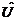 ) von der anregenden Frequenz (Erregerfrequenz)
) von der anregenden Frequenz (Erregerfrequenz)  abhängig ist. Ist die
anregende Frequenz oder Erregerfrequenz im Bereich der Eigenfrequenz des
Schwingkreises
abhängig ist. Ist die
anregende Frequenz oder Erregerfrequenz im Bereich der Eigenfrequenz des
Schwingkreises oder
oder  (Kreisfrequenz), so ist die Amplitude der Schwingung sehr
groß. Sollte keine Dämpfung vorhanden sein, führt dies in der Regel zu einer
Resonanzkatastrophe, das würde bedeuten, dass
(Kreisfrequenz), so ist die Amplitude der Schwingung sehr
groß. Sollte keine Dämpfung vorhanden sein, führt dies in der Regel zu einer
Resonanzkatastrophe, das würde bedeuten, dass  ist und die
Eigenschwingung f des Schwingkreises
würde immer größere Amplituden vorweisen (s.Abb.2) .
Die Dämpfung der periodischen Schwingung hängt ebenfalls vom Wirkwiderstand
(Realteil des komplexen Wechselstromwiderstandes) der Spule ab. Deshalb spricht
man erst dann von einem Resonanzkreis wenn man eine Spule, einen Kondensator
und einen ohmschen Widerstand in Reihe schaltet. Da bei gleicher
Generatorspannung
ist und die
Eigenschwingung f des Schwingkreises
würde immer größere Amplituden vorweisen (s.Abb.2) .
Die Dämpfung der periodischen Schwingung hängt ebenfalls vom Wirkwiderstand
(Realteil des komplexen Wechselstromwiderstandes) der Spule ab. Deshalb spricht
man erst dann von einem Resonanzkreis wenn man eine Spule, einen Kondensator
und einen ohmschen Widerstand in Reihe schaltet. Da bei gleicher
Generatorspannung  die Stromstärke I variabel ist (denn sie ist abhängig
von der Erregerfrequenz
die Stromstärke I variabel ist (denn sie ist abhängig
von der Erregerfrequenz ), spricht man bei
), spricht man bei  von der
Eigenfrequenz f des Schwingkreises und der
Resonanz. Denn der Schwingkreis wird dann mit seinen Eigenfrequenzen angeregt
und es tritt Resonanz (konstante Amplitude sowie Frequenz) ein .
Fazit man unterscheidet also gedämpfte Schwingungen und ungedämpfte
Schwingungen (vgl.Abb.3, S.4).
von der
Eigenfrequenz f des Schwingkreises und der
Resonanz. Denn der Schwingkreis wird dann mit seinen Eigenfrequenzen angeregt
und es tritt Resonanz (konstante Amplitude sowie Frequenz) ein .
Fazit man unterscheidet also gedämpfte Schwingungen und ungedämpfte
Schwingungen (vgl.Abb.3, S.4).
|

|
Abb.2
Stromresonanz
eines Schwingkreises in Abhängigkeit
der Dämpfung (ohmscher Widerstand, Wirkwiderstand der Spule) Quelle:
iva.uni-ulm.de/PHYSIK/VORLESUNG/ELEHRE/node131.html (ebenfalls Abb.1
entnommen)
|
|
|
|
|
| | | |
 Da man aufgrund der
anregenden Frequenz
Da man aufgrund der
anregenden Frequenz  die Eigenfrequenz f
des Schwingkreises bestimmen kann, indem man ihm eine bestimmte Verstärkung im
Takt der Eigenfrequenz f zuführt und
somit die Amplitude der Schwingung konstant hält, ist es möglich einen
Resonanzkreis als Filter in der Rundfunktechnik einzusetzen. Man könnte so die
gewünschte Trägerfrequenz, die Frequenz die ein Sender absendet, herausfiltern,
d.h. die Trägerfrequenz muss mit der Eigenfrequenz des Empfängers
übereinstimmen, damit sie weitergeleitet werden kann, so lassen sich aus
verschieden Trägerfrequenzen die gewünschten Frequenzen herausselektieren
(Vertiefung s. Kapitel 5, "Nutzung
der elektromagnetischen Welle in der Rundfunktechnik").
die Eigenfrequenz f
des Schwingkreises bestimmen kann, indem man ihm eine bestimmte Verstärkung im
Takt der Eigenfrequenz f zuführt und
somit die Amplitude der Schwingung konstant hält, ist es möglich einen
Resonanzkreis als Filter in der Rundfunktechnik einzusetzen. Man könnte so die
gewünschte Trägerfrequenz, die Frequenz die ein Sender absendet, herausfiltern,
d.h. die Trägerfrequenz muss mit der Eigenfrequenz des Empfängers
übereinstimmen, damit sie weitergeleitet werden kann, so lassen sich aus
verschieden Trägerfrequenzen die gewünschten Frequenzen herausselektieren
(Vertiefung s. Kapitel 5, "Nutzung
der elektromagnetischen Welle in der Rundfunktechnik").
2.1. Phasenbeziehungen im
Schwingkreis
Nehmen wir an, dass
der Kondensator C zu Beginn der
Schwingungsperiode auf die Spannung  aufgeladen ist und es
fließt zunächst kein Strom (ohmscher Widerstand vernachlässigt). Daraufhin
entlädt sich der Der Kondensator durch die Spule L in der sich ein Magnetfeld mit der Feldstärke B=
aufgeladen ist und es
fließt zunächst kein Strom (ohmscher Widerstand vernachlässigt). Daraufhin
entlädt sich der Der Kondensator durch die Spule L in der sich ein Magnetfeld mit der Feldstärke B= aufbaut. Nach
aufbaut. Nach  (T = Periodendauer
einer Schwingung) hat sich der Kondensator entladen. Die gesamte in ihm
gespeicherte Energie
(T = Periodendauer
einer Schwingung) hat sich der Kondensator entladen. Die gesamte in ihm
gespeicherte Energie 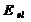 =
=  ist nun im Magnetfeld
der Spule enthalten, welche nun
ist nun im Magnetfeld
der Spule enthalten, welche nun 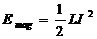 beträgt. Setzt man
beträgt. Setzt man 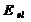 und
und  gleich und formt um
(eliminiert man), so erhält man für die nun maximale Stromstärke,
gleich und formt um
(eliminiert man), so erhält man für die nun maximale Stromstärke,
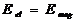

 =
= 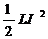

 =
=  |
| 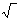

 =
= 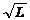
 |
| 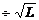




Das erzeugte
Magnetfeld wird nun abgebaut, indem in die Spule L eine Spannung induziert wird, dieser Vorgang bewirkt wiederum,
dass der Kondensator C mit
umgekehrtem Vorzeichen aufgeladen wird. Nach  beträgt die Spannung
am Kondensator C erneut
beträgt die Spannung
am Kondensator C erneut  und folglich ist die
Stromstärke I, sowie die magnetische Energie
und folglich ist die
Stromstärke I, sowie die magnetische Energie  gleich 0. Daraufhin wiederholt sich der bis hierin
beschriebene Vorgang, bis der Ausgangszustand nach einer Schwingungsdauer T gegeben ist. Vergleicht man die einzelnen Phasen des elektrischen
Schwingkreises mit der der mechanischen
Schwingung, so lassen sich folgende Übereinstimmungen feststellen:
gleich 0. Daraufhin wiederholt sich der bis hierin
beschriebene Vorgang, bis der Ausgangszustand nach einer Schwingungsdauer T gegeben ist. Vergleicht man die einzelnen Phasen des elektrischen
Schwingkreises mit der der mechanischen
Schwingung, so lassen sich folgende Übereinstimmungen feststellen:
 ;
;  ;
;  ;
; 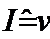 ;
; 
Es bedeutet:
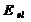 = elektrische Energie ; v = Geschwindigkeit der
Schwingung
= elektrische Energie ; v = Geschwindigkeit der
Schwingung
 = potenzielle Energie ; Q = transportierte Ladungen
= potenzielle Energie ; Q = transportierte Ladungen
 = magnetische Energie ; I = Stromstärke
= magnetische Energie ; I = Stromstärke
 = kinetische Energie ;
= kinetische Energie ;  Ausgangsspannung ;
Ausgangsspannung ;  = Rücktreibende
Kraft
= Rücktreibende
Kraft
3. Ungedämpfte elektrische
Schwingungen
Bei ungedämpften elektrischen Schwingkreisen bleibt die Amplitude der Schwingung zeitlich
konstant, dass heißt
der Widerstand R (Dämpfung) ist gleich 0 und Strom- sowie Spannungsverlauf sind sinusförmig. Das
Abklingen der Schwingungen in gedämpften Schwingkreisen kann durch die
folgenden Schaltungen unterbunden werden. Des Weiteren wird die entstehende
Energie in Form von elektromagnetischen
Wellen abgestrahlt.
und Strom- sowie Spannungsverlauf sind sinusförmig. Das
Abklingen der Schwingungen in gedämpften Schwingkreisen kann durch die
folgenden Schaltungen unterbunden werden. Des Weiteren wird die entstehende
Energie in Form von elektromagnetischen
Wellen abgestrahlt.
3.1. Meissner-Schaltung
Am Anfang des 20.Jahrhunderts "entwickelte der deutsche Physiker Alexander Meissner (1883-1958) eine Rückkopplungsschaltung, die die Erzeugung ungedämpfter
elektromagnetischer Schwingungen ermöglichte. Mit der ersten Sendung am
29.10.1923 begann die Entwicklung des öffentlichen Rundfunks in Deutschland,
467 registrierte Teilnehmer hörten diese erste Rundfunkübertragung" .
Mit Hilfe dieser Schaltung lassen sich Schwingungen
"entdämpfen", was bedeutet, dass die Amplitude der Trägerfrequenzen konstant
bleibt. Betrachtet man die Oszillatorschaltung
nach Meissner (Abb.4,S.6), handelt es sich um eine transformatorische
Rückkopplungsschaltung, Rückkopplungsschaltung aus dem Grunde, da man um die
Schwingung aufrechtzuerhalten dem Schwingkreis im richtigen Moment Energie
zuführt, die an dem Widerstand der realen Spule  verloren geht. Somit
liegt ein ungedämpfter Oszillator bzw. ein Hochfrequenz-Oszillator vor, da der
Kreis sozusagen ständig entdämpft wird. Grundsätzlich verwendet man einen
Parallelschwingkreis, bestehend aus dem Kondensator C und der Spule
verloren geht. Somit
liegt ein ungedämpfter Oszillator bzw. ein Hochfrequenz-Oszillator vor, da der
Kreis sozusagen ständig entdämpft wird. Grundsätzlich verwendet man einen
Parallelschwingkreis, bestehend aus dem Kondensator C und der Spule , der mit Hilfe
eines npn-Transistors angeregt wird. Angenommen es ist bereits eine elektrische
Schwingung im Schwingkreis angeregt, so induziert die Spule
, der mit Hilfe
eines npn-Transistors angeregt wird. Angenommen es ist bereits eine elektrische
Schwingung im Schwingkreis angeregt, so induziert die Spule  (Spule des
Schwingkreises/Schwingkreisspule) in die Induktionsspule
(Spule des
Schwingkreises/Schwingkreisspule) in die Induktionsspule  eine Wechselspannung mit der Eigenfrequenz f des Schwingkreises, da
eine Wechselspannung mit der Eigenfrequenz f des Schwingkreises, da  und
und  mit einem Eisenkern
verbunden sind und somit einen Transformator
bilden, aus diesem Grund auch transformatorische Rückkopplung genannt. Die
Induktionsspule
mit einem Eisenkern
verbunden sind und somit einen Transformator
bilden, aus diesem Grund auch transformatorische Rückkopplung genannt. Die
Induktionsspule  sendet nun das
entsprechende positive "Signal"
an die Basis des npn-Transistors. Denn die Entladung des Kondensators führt zu einem
Stromfluss und somit zum Aufbau eines Magnetfeldes um die Primärspule
sendet nun das
entsprechende positive "Signal"
an die Basis des npn-Transistors. Denn die Entladung des Kondensators führt zu einem
Stromfluss und somit zum Aufbau eines Magnetfeldes um die Primärspule , da die Induktionsspule von diesem Magnetfeld durchsetzt wird
kommt es, wie gesagt, zur Induktion einer Spannung in die Induktionsspule .
Folglich wird der Transistor leitend, d.h. Emitter-Kollektor-Strom fließt mit
der Frequenz f des Schwingkreises und es
kann eine ungedämpfte Schwingung aufrechterhalten werden, denn es ist
, da die Induktionsspule von diesem Magnetfeld durchsetzt wird
kommt es, wie gesagt, zur Induktion einer Spannung in die Induktionsspule .
Folglich wird der Transistor leitend, d.h. Emitter-Kollektor-Strom fließt mit
der Frequenz f des Schwingkreises und es
kann eine ungedämpfte Schwingung aufrechterhalten werden, denn es ist  =
= .
Der Spannungsteiler, bestehend aus
.
Der Spannungsteiler, bestehend aus  und
und  , verhindert zum einen eine Übersteuerung und begrenzt den
Basisstrom um das richtige "Signal" zu erhalten, zum anderen reicht bereits
eine kleine induzierte Spannung aus, um
den Transistor zu schalten.
, verhindert zum einen eine Übersteuerung und begrenzt den
Basisstrom um das richtige "Signal" zu erhalten, zum anderen reicht bereits
eine kleine induzierte Spannung aus, um
den Transistor zu schalten.
|

|
Abb.4
Rückkopplungsschaltung nach
Meissner
(in original Schaltung mit Triode)
|
3.2 Dreipunktschaltung
Die Dreipunktschaltung stellt eine Erweiterung der
Rückkopplungsschaltung nach Meissner
und einen Hochfrequenz-Oszillator dar,
mit dem elektromagnetische Wellen (insbesondere Radiowellen) erzeugt werden
können. Doch es gibt gewisse Veränderungen die Dreipunktschaltung und
Rückkopplungsschaltung nach Meissner
unterscheiden. Je nach dem welches Bauteil (Spule oder Kondensator) zur
Rückkopplung benutzt wird, unterscheidet man zwischen der induktiven
Dreipunktschaltung und der kapazitiven Dreipunktschaltung. Die
Dreipunktschaltung soll nun am Beispiel eines Dreipunkt-Oszillators, also einer
induktiven Dreipunktschaltung erklärt werden. Zunächst entfällt die
Induktionsspule , also erfolgt die Rückkopplung über einen direktem Abgriff
an der Spule
, also erfolgt die Rückkopplung über einen direktem Abgriff
an der Spule 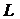 (der Spule des Schwingkreises) ,
dazu wird die hier entstehende Teilspannung
(der Spule des Schwingkreises) ,
dazu wird die hier entstehende Teilspannung  genutzt, während beim Meissner-Oszillator zur Rückkopplung ein Übertrager (2
Spulen) genutzt wird.
genutzt, während beim Meissner-Oszillator zur Rückkopplung ein Übertrager (2
Spulen) genutzt wird.
 Der
Name Dreipunktschaltung wird für
diese Art Schaltung benutzt, da eine Spule verwendet wird, an der man an drei Punkten abgreifen kann.
Der Transistor T hat dieselbe Funktion, wie der npn-Transistor in Abb.4, denn er wird vom Koppelkondensator C2 angesteuert. Über den Transistor T erhält der LC-Schwingkreis
die optimale Verstärkung, um die Schwingung konstant zu halten. Mit Hilfe des
Drehkondensators lässt sich die Frequenz des Schwingkreises und somit die
Frequenz der abgestrahlten Radiowelle
variieren, was sich wiederum mit der Thomson'schen
Gleichung begründen lässt (s. Kapitel 2). Die vom Oszillator erzeugte
Radiowelle kann nun über die Antenne abgestrahlt werden. Der y-Ausgang stellt
den Anschluss eines Oszilloskops dar, mit dem man die erzeugten Frequenzen
sichtbar machen kann. Empfangen kann man diese Wellen mit einem einfachen
Diodenempfänger (Resonanzkreis + HF Diode), den man auf die Sendefrequenz
abstimmt, indem man mit einem Drehkondensator die entsprechende Frequenz des
Resonanzkreises ermittelt und die empfangenen Frequenzen, nach Gleichrichtung
der HF-Diode, über einen Verstärker, mit einem Lautsprecher hörbar macht.
Der
Name Dreipunktschaltung wird für
diese Art Schaltung benutzt, da eine Spule verwendet wird, an der man an drei Punkten abgreifen kann.
Der Transistor T hat dieselbe Funktion, wie der npn-Transistor in Abb.4, denn er wird vom Koppelkondensator C2 angesteuert. Über den Transistor T erhält der LC-Schwingkreis
die optimale Verstärkung, um die Schwingung konstant zu halten. Mit Hilfe des
Drehkondensators lässt sich die Frequenz des Schwingkreises und somit die
Frequenz der abgestrahlten Radiowelle
variieren, was sich wiederum mit der Thomson'schen
Gleichung begründen lässt (s. Kapitel 2). Die vom Oszillator erzeugte
Radiowelle kann nun über die Antenne abgestrahlt werden. Der y-Ausgang stellt
den Anschluss eines Oszilloskops dar, mit dem man die erzeugten Frequenzen
sichtbar machen kann. Empfangen kann man diese Wellen mit einem einfachen
Diodenempfänger (Resonanzkreis + HF Diode), den man auf die Sendefrequenz
abstimmt, indem man mit einem Drehkondensator die entsprechende Frequenz des
Resonanzkreises ermittelt und die empfangenen Frequenzen, nach Gleichrichtung
der HF-Diode, über einen Verstärker, mit einem Lautsprecher hörbar macht.
4. Die elektromagnetische Welle
Zunächst bezeichnet man elektromagnetische Felder, die
bei allen beschleunigten sowie negativ beschleunigten Ladungsträgern frei
werden, als elektromagnetische Wellen, da sich die Stärken des elektrischen-
bzw. magnetischen Feldes "sowohl räumlich als auch zeitlich periodisch"
und zwar wellenförmig ändern.
Die untersuchten HF-Oszillatoren und vor allem die
Dreipunktschaltung zeigen, dass elektromagnetische Wellen dort entstehen, wo
die Richtung des Stromflusses I periodisch
geändert wird, denn bei dieser Richtungsänderung werden Elektronen im
Leitungsdraht beschleunigt. Die Entstehung einer elektromagnetischen Welle
lässt sich auf folgende Weise erläutern: Angenommen durch einen Sendedipol
(langer Draht, Antenne die mit einem HF-Oszillator verbunden ist und (Spule))
fließt ein periodischer Wechselstrom, dann baut sich ein kreisförmiges
Magnetfeld, mit der magnetischen Flussdichte  und der Einheit [B]
und der Einheit [B]
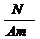 =1 Tesla, dessen Ausrichtung (Orientierung) von der
Stromrichtung vorgegeben wird, auf. Aufgrund der Phasenverschiebung kommt
dieses Magnetfeld, in der Zeit
=1 Tesla, dessen Ausrichtung (Orientierung) von der
Stromrichtung vorgegeben wird, auf. Aufgrund der Phasenverschiebung kommt
dieses Magnetfeld, in der Zeit 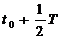 (T
(T  Periodendauer der Schwingung), zwei mal zum erliegen, da sich
bei diesem Prozess ein ständiger Auf- und Abbau von magnetischer- und
elektrischer Feldenergie
Periodendauer der Schwingung), zwei mal zum erliegen, da sich
bei diesem Prozess ein ständiger Auf- und Abbau von magnetischer- und
elektrischer Feldenergie 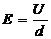 (da Kondensator
(da Kondensator homogenes Feld, [E]=1
homogenes Feld, [E]=1 ) vollzieht, geht man davon aus, dass ein periodisches
elektromagnetisches Wechselfeld entsteht. Dieses Feld (elektromagnetische
Welle) ist in der Lage sich von der Oberfläche des Sendedipols zu lösen, wobei
sich diese elektromagnetische Welle, die sowohl aus einem elektrischen
Feld, als auch magnetischen Feld
besteht, "dessen Feldstärken E und B
senkrecht zueinander polarisiert sind" ,
mit der Lichtgeschwindigkeit c
) vollzieht, geht man davon aus, dass ein periodisches
elektromagnetisches Wechselfeld entsteht. Dieses Feld (elektromagnetische
Welle) ist in der Lage sich von der Oberfläche des Sendedipols zu lösen, wobei
sich diese elektromagnetische Welle, die sowohl aus einem elektrischen
Feld, als auch magnetischen Feld
besteht, "dessen Feldstärken E und B
senkrecht zueinander polarisiert sind" ,
mit der Lichtgeschwindigkeit c (
(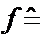 der Frequenz der Welle und
der Frequenz der Welle und  der Wellenlänge)
ausbreitet. Die Lichtgeschwindigkeit (im Vakuum) stellt eine Naturkonstante dar
und es gilt,
der Wellenlänge)
ausbreitet. Die Lichtgeschwindigkeit (im Vakuum) stellt eine Naturkonstante dar
und es gilt,  .Die
Ausbreitungsgeschwindigkeit aller elektromagnetischen Wellen im Vakuum lässt
sich mit Hilfe der Formel
.Die
Ausbreitungsgeschwindigkeit aller elektromagnetischen Wellen im Vakuum lässt
sich mit Hilfe der Formel 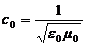 bestimmen, "aus dieser
Gleichung folgt, dass alle elektromagnetischen Wellen die gleiche
Ausbreitungsgeschwindigkeit besitzen" ,
sie ist identisch mit der Vakuumlichtgeschwindigkeit. Doch betrachtet man die
Ausbreitungsgeschwindigkeit in Stoffen, dürfen "die durch
bestimmen, "aus dieser
Gleichung folgt, dass alle elektromagnetischen Wellen die gleiche
Ausbreitungsgeschwindigkeit besitzen" ,
sie ist identisch mit der Vakuumlichtgeschwindigkeit. Doch betrachtet man die
Ausbreitungsgeschwindigkeit in Stoffen, dürfen "die durch 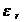 und
und  veränderten
Feldstärken"
nicht Außeracht gelassen werden, denn es gilt
veränderten
Feldstärken"
nicht Außeracht gelassen werden, denn es gilt 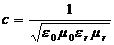 , da bereits aufgezeigt wurde, dass
, da bereits aufgezeigt wurde, dass  ist kann man sie in
die Gleichung für die Ausbreitungsgeschwindigkeit in Stoffen einsetzen und man
erhält
ist kann man sie in
die Gleichung für die Ausbreitungsgeschwindigkeit in Stoffen einsetzen und man
erhält  . Aufgrund der Tatsache, dass für die meisten Stoffe, außer
für ferromagnetische Stoffe,
. Aufgrund der Tatsache, dass für die meisten Stoffe, außer
für ferromagnetische Stoffe,  gilt, erhält man für c der elektromagnetischen Wellen in Stoffen
gilt, erhält man für c der elektromagnetischen Wellen in Stoffen
 .
.
Für die Gleichungen gelten:
Elektrische Feldkonstante ..8,854187817
..8,854187817
Magnetische Feldkonstante  .......1,2566370614
.......1,2566370614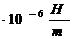 = 4
= 4
Permittivitätszahl (Dielektrizitätszahl)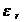 ...1
...1
Permeabilitätszahl  .........1
.........1
(Konstanten sind dem Tafelwerk entnommen,
Buchdeckelinnenseite und S.61)
 Die folgende Tabelle soll zum einen die identische und
konstante Ausbreitungsgeschwindigkeit von
Licht-, Hertz'schen Wellen (Lang-, Mittel-, Kurz-, Ultrakurz- und Mikrowellen) und
Röntgendstrahlung, aber auch die aufgeführten Gleichungen veranschaulichen.
Die folgende Tabelle soll zum einen die identische und
konstante Ausbreitungsgeschwindigkeit von
Licht-, Hertz'schen Wellen (Lang-, Mittel-, Kurz-, Ultrakurz- und Mikrowellen) und
Röntgendstrahlung, aber auch die aufgeführten Gleichungen veranschaulichen.
Die Eigenschaften der elektromagnetischen Welle sind
gleich denen, die als charakteristische Merkmale von Wellen bezeichnet werden.
Hierzu Zählen die Reflexion, die Brechung, die Beugung und die Interferenz (Das
Überlagern von Schwingungen man unterscheidet konstruktive-(maximale
Verstärkung) und destruktive (max. Abschwächung der Schwingung) Interferenz).
Weiterhin kann eine elektromagnetische Welle, unter Anwendung von Polarisatoren,
polarisiert werden ,
daraus folgt, dass die Schwingung der elektrischen Feldstärke 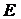 bei polarisierten
Wellen vorgegeben ist, also eine bestimmte Richtung besitzt. Im Allgemeinen
unterscheidet man vier Klassifizierungen elektromagnetischer Welle, die da
sind, Röntgenstrahlung, die z.B. in der Natur entsteht, wenn Ladungsträger
beschleunigt und wieder abgebremst werden. Des Weiteren unterscheidet man die
langwelligeren sichtbaren bis hin zu infraroten elektromagnetischen Wellen, die
beim Rotieren oder Schwingen von Molekülen entstehen, zudem sendet die Sonne
ebenfalls ein erhebliches Spektrum elektromagnetischer Wellen, wovon das menschliche Auge aber nur den
sichtbaren Teil wahrnimmt, ab.
bei polarisierten
Wellen vorgegeben ist, also eine bestimmte Richtung besitzt. Im Allgemeinen
unterscheidet man vier Klassifizierungen elektromagnetischer Welle, die da
sind, Röntgenstrahlung, die z.B. in der Natur entsteht, wenn Ladungsträger
beschleunigt und wieder abgebremst werden. Des Weiteren unterscheidet man die
langwelligeren sichtbaren bis hin zu infraroten elektromagnetischen Wellen, die
beim Rotieren oder Schwingen von Molekülen entstehen, zudem sendet die Sonne
ebenfalls ein erhebliches Spektrum elektromagnetischer Wellen, wovon das menschliche Auge aber nur den
sichtbaren Teil wahrnimmt, ab.
5. Nutzung der elektromagnetischen
Welle in der Rundfunktechnik
In der Rundfunktechnik hat man sich die Eigenschaften
der elektromagnetischen Wellen zunutze gemacht, um Informationen, wie zum
Beispiel Sprache oder Musik drahtlos, von einem Punkt A zu einem Punkt B,
übertragen zu können.
In den weiteren Unterpunkten soll nun geklärt werden,
wie elektromagnetische Wellen diese Informationen übertragen können und wie sie
transportiert werden.
5.1. Modulation und Demodulation
Wie in Kapitel 5 beschrieben, können
elektromagnetische Wellen Informationen, wie zum Beispiel Sprache oder Musik,
übertragen. Die Hochfrequenz- (HF-) Schwingung, die bei den
Hochfrequenz-Oszillatoren (Meissner-Rückkopplungsschaltung
und der Dreipunktschaltung) abgestrahlt wird, nennt man Trägerfrequenz. Doch
allein diese Trägerfrequenz erzeugt im Empfangsgerät keine Audiosignale, in
Form von Musik etc., ihr muss gewissermaßen eine Information angepasst werden
und eben diesen Vorgang nennt man Modulation, denn Modulieren bedeutet, die
Trägerfrequenz so zu verändern, dass zum Beispiel die gewünschte Tonhöhe oder
Lautstärke einer bestimmten Nachricht gesendet wird. So wird der
Trägerwelle sozusagen eine
niederfrequente Schwingung "aufgeprägt" . In der Rundfunktechnik haben sich zwei
verschiedene analoge Modulationsarten durchgesetzt und zwar die Amplituden- und
Frequenzmodulation, die im Folgenden näher erläutert werden sollen. Vorweg sei
gesagt, dass die Lautstärke, des zu übertragenden Tons, ein Maß für Amplituden-
bzw. Frequenzänderungen darstellt. Da man, um Musik zu übertragen, höhere Frequenzen benötigt, benutzt man das
Frequenzband von 30 bis 18000Hz, dieses Band macht gleichzeitig den gesamten
hörbaren Bereich aus, während zur Übertragung von Sprache ein Frequenzband von
300 bis 3400Hz ausreichend ist (Telefon). Bei Fernsehgeräten bedient man sich
der Frequenzen von 0 bis 5MHz.
Demodulation erfolgt, indem man einen Resonanzkreis
(als Filter) auf die Frequenz einer HF- oder Trägerschwingung (hochfrequente
Schwingung) abstimmt, mittels einer Diode kann das übertragende Signal
gleichgerichtet werden und über einen Verstärker kann man dieses Signal zum
Beispiel einem Lautsprecher zu fügen. Da es sich um eine hochfrequente
Schwingung handelt kann diese nicht direkt von der trägen Membran eines
Lautsprechers hörbar gemacht werden. Die Amplitude der HF-Schwingung, die sich
im Takt der Niederfrequenz ändert (Amplitudenmodulation) oder die
Frequenzunterschiede, bei gleicher Amplitudenhöhe (Frequenzmodulation), können
mit Hilfe eines Drehspulinstruments (Messgerät o. Oszilloskop) gemessen werden.
Weitere Modulationsarten sind Pulsamplitudenmodulation(PAM),
Pulsdauermodulation(PDM), Pulsphasenmodulation(PPM), Pulscodemodulation(PCM)
sowie die Phasenmodulation(PM). Während es sich bei der Phasenmodulation um
eine weitere analoge Modulationsart handelt, sind Pulsamplitudenmodulation,
Pulsdauermodulation, Pulsphasenmodulation und die Pulscodemodulation digitale
Modulationen, bei denen die Signalwellen (digitale Signale) kurze Zeitschlitze
für ihre Übertragung nutzen, so steht ihnen die gesamte Bandbreite
(Frequenzbereich) ständig zur Verfügung, während zum Beispiel UKW-Sender (FM)
an einen bestimmten Übertragungskanal gebunden sind.
5.1.1 Amplitudenmodulation
(AM)
Das Prinzip der Amplitudenmodulation besteht darin,
die Amplitude der Trägerfrequenz, also der HF- Schwingung, im Takt der
Niederfrequenz
leicht zu verändern, indem man unter Verwendung eines Modulationsgrads (max.
Verhältnis Signalamplitude zur Trägeramplitude) von ca. 30%, da Modulation von
über 100% zu Verzerrungen führen ,
die Trägerfrequenz dem Modulationssignal anpasst. Der Modulationsgrad stellt
einen Parameter dar und lässt sich mit Hilfe der Formel,
m ermitteln,
ermitteln,
darin gilt:  = Spitzenwert des unmodulierten Trägers
= Spitzenwert des unmodulierten Trägers
 = Spitzenwert des
modulierten Trägers
= Spitzenwert des
modulierten Trägers
 Die Trägerfrequenz selbst enthält keine Informationen, da
alle Amplituden gleich hoch sind. Nach der Modulation der Amplituden beschreiben
die Amplitudenspitzen (untere, sowie obere) eine Wellenlinie, die der
Wellenlinie, z.B. der Niederfrequenz, entspricht (Abb.6). Vereinfacht
ausgedrückt lässt sich sagen, dass die Amplitudenhöhen am Rundfunkgerät kontinuierlich, aber leicht
im Rhythmus der Niederfrequenz schwanken. Im Radiogerät müssen nun diese feinen
Schwankungen heraus- gefiltert werden, diesen Vorgang nennt man Demodulation
(s.5.1.), die herausgefilterten Signale werden daraufhin verstärkt und mittels
Lautsprecher hörbar. Das Verfahren der Amplitudenmodulation wird bei Lang-,
Mittel-, und Kurzwelle angewandt, doch es besteht ein gewisser Nachteil, für
zum Beispiel den Radiohörer, denn amplitudenmodulierte elektromagnetische
Wellen sind sehr störanfällig. Das heißt, die Empfangsstärke (Amplitude der
Trägerfrequenz) wird durch Störungen, wie z.B. Gewitter oder Oberleitungen, so
beeinflusst, dass Informationen oftmals nicht mehr vorhanden sind, da sich die
Amplitudenhöhen verändert haben. Doch ein Vorteil der Amplitudenmodulation ist die
sehr hohe Reichweite dieser Radiowelle, welche auf dem Phänomen der Raumwelle
(Radiowellen, die von der Ionosphäre reflektiert werden
) beruht.
Die Trägerfrequenz selbst enthält keine Informationen, da
alle Amplituden gleich hoch sind. Nach der Modulation der Amplituden beschreiben
die Amplitudenspitzen (untere, sowie obere) eine Wellenlinie, die der
Wellenlinie, z.B. der Niederfrequenz, entspricht (Abb.6). Vereinfacht
ausgedrückt lässt sich sagen, dass die Amplitudenhöhen am Rundfunkgerät kontinuierlich, aber leicht
im Rhythmus der Niederfrequenz schwanken. Im Radiogerät müssen nun diese feinen
Schwankungen heraus- gefiltert werden, diesen Vorgang nennt man Demodulation
(s.5.1.), die herausgefilterten Signale werden daraufhin verstärkt und mittels
Lautsprecher hörbar. Das Verfahren der Amplitudenmodulation wird bei Lang-,
Mittel-, und Kurzwelle angewandt, doch es besteht ein gewisser Nachteil, für
zum Beispiel den Radiohörer, denn amplitudenmodulierte elektromagnetische
Wellen sind sehr störanfällig. Das heißt, die Empfangsstärke (Amplitude der
Trägerfrequenz) wird durch Störungen, wie z.B. Gewitter oder Oberleitungen, so
beeinflusst, dass Informationen oftmals nicht mehr vorhanden sind, da sich die
Amplitudenhöhen verändert haben. Doch ein Vorteil der Amplitudenmodulation ist die
sehr hohe Reichweite dieser Radiowelle, welche auf dem Phänomen der Raumwelle
(Radiowellen, die von der Ionosphäre reflektiert werden
) beruht.
5.1.2 Frequenzmodulation
(FM)
 Die Frequenzmodulation findet vorwiegend im UKW-Bereich
Anwendung, dies macht sich außerdem dadurch bemerkbar, dass auf sämtlichen
Skalen FM (Frequency Modulation) anstatt UKW aufgeführt wird. Bei der
Frequenzmodulation wird die Trägerfrequenz selbst und nicht ihre Amplitude im
Takt des Niederfrequenzsignals verändert. Während der eigentliche, nicht modulierte HF-Träger
(Trägerfrequenz/HF-Schwingung) eine regelmäßige Frequenz hat, besitzt die
Frequenzmodulierte Hochfrequenz verschiedene Abstände, d.h. ihre Frequenz
schwankt bei gleicher Amplitudenhöhe, oder sie wird im Takt der Tonschwingung
vergrößert bzw. verkleinert (Abb.7). Diese in den Frequenzschwankungen
enthaltene Informationen müssen wie bei der Amplitudenmodulation im
Empfangsgerät (Radiogerät) herausgefiltert werden, d.h. demoduliert, verstärkt
und mittels Lautsprecher hörbar gemacht werden. Frequenzmodulierte Schwingungen
(Signale) bieten Vorteile bei der Informationsübertragung von Musik etc., da
sie weniger störanfällig sind doch der größte Nachteil ist jedoch, die relativ
kurze Reichweite, die aus der Verwendung von Bodenwellen (Rundfunkwelle, die
sich längs des Erdboden ausbreitet )
resultiert, die wiederum von kleineren Unebenheiten aufgehalten werden (z.B.
Gebirge, Hochhäuser usw.).
Die Frequenzmodulation findet vorwiegend im UKW-Bereich
Anwendung, dies macht sich außerdem dadurch bemerkbar, dass auf sämtlichen
Skalen FM (Frequency Modulation) anstatt UKW aufgeführt wird. Bei der
Frequenzmodulation wird die Trägerfrequenz selbst und nicht ihre Amplitude im
Takt des Niederfrequenzsignals verändert. Während der eigentliche, nicht modulierte HF-Träger
(Trägerfrequenz/HF-Schwingung) eine regelmäßige Frequenz hat, besitzt die
Frequenzmodulierte Hochfrequenz verschiedene Abstände, d.h. ihre Frequenz
schwankt bei gleicher Amplitudenhöhe, oder sie wird im Takt der Tonschwingung
vergrößert bzw. verkleinert (Abb.7). Diese in den Frequenzschwankungen
enthaltene Informationen müssen wie bei der Amplitudenmodulation im
Empfangsgerät (Radiogerät) herausgefiltert werden, d.h. demoduliert, verstärkt
und mittels Lautsprecher hörbar gemacht werden. Frequenzmodulierte Schwingungen
(Signale) bieten Vorteile bei der Informationsübertragung von Musik etc., da
sie weniger störanfällig sind doch der größte Nachteil ist jedoch, die relativ
kurze Reichweite, die aus der Verwendung von Bodenwellen (Rundfunkwelle, die
sich längs des Erdboden ausbreitet )
resultiert, die wiederum von kleineren Unebenheiten aufgehalten werden (z.B.
Gebirge, Hochhäuser usw.).
|
Frequenzübersicht
|
|
|
Anwendung
|
Frequenzbereich
|
|
1.Heilberufe
|
151-152 MHz
|
|
2.CB Funk
|
26-28 MHz
|
|
2m Band/Amateurfunk
|
144-146 MHz
|
|
70 cm Band/Amateurfunk
|
430-440 MHz
|
|
3.Funktaxi
|
147-164 MHz
|
|
4.Handwerks und
Industriebetriebe
|
148-156 MHz
|
|
5.Mobilfunk A-Netz
|
150-MHz-Bereich
|
|
B-Netz
|
148,40-149,18 MHz
; 153,00-153,78 MHz
|
|
B2-Netz
|
157,60-158,34 MHz
; 162,20-162,94 MHz
|
|
C-Netz
|
451,30-455,74 MHz
; 461,30-465,74 MHz
|
|
6.Motorsport
|
147-160 MHz
|
|
7.Polizei
|
84-87 MHz
|
|
8.Rettungsleitstellen
|
84-87 MHz
|
|
9.Feuerwerk
|
84-87 MHz
|
|
10.Flugfunk
|
118-136 MHz
|
|
11.Seefunk
|
156-162 MHz
|
|
12.Zugfunk
|
70-71 MHz
|
|
|
80-81 MHz
|
|
|
457-468 MHz
|
|
13.Militärfunk
|
30-47 MHz
|
|
14.Mobilfunk D-
und E-Netz
|
880-960 MHz
|
|
|
1710-1880 MHz
|
|
|
1850-1990 MHz
|
|
15.UMTS
|
1885-2025 MHz
|
|
|
2110-2200 MHz
|
|
16.Drahtlose
Mikrofone
|
30-39 MHz
|
|
|
198-830 MHz
|
|
|
174-175 MHz
|
|
17.Schnurlose
Telefone
|
832-930 MHz
|
|
|
1880-1900 MHz
|
|
18.Cityruf (Pager)
|
465,970-466,230 MHz
|
| | |
Daten entnommen aus: Geist, Hans-Joachim: Großes
Praxisbuch der Kommunikationstechnik S.269 ff ; Tabelle dient dazu, genannte
Frequenzbereiche einordnen zu können, sowie dem Leser einen groben Überblick
über alltägliche Frequenzbereiche zu gewährleisten.
6. Literaturverzeichnis
Primärliteratur:
Bader, Professor Dr. Franz, Dorn-Bader, Schroedel Verlag, Physik
Gymnasium Sek II 12/13, 2003
Das große Tafelwerk, Volk und Wissen, Formelsammlung für die Sekundarstufe I und
II, 2002, 1.Auflage
Geist, Hans Joachim: Großes
Praxisbuch der Kommunikation, Elektor Verlag, 2001
Gölz, Rainer: cb-funkfibel,
Albrecht Philler Verlag
Gölz, Rainer: cb-funkpraxis,
Albrecht Philler Verlag
Grehn J., Krause J.(Hrsg.): Metzler Physik, Metzler Verlag, 1998, 3.Auflage
Hartmann, Prof. Dr. Elke, Hein, Prof. Dr. Christian: Duden Technik, Paetec Verlag,
Basiswissen Schule (Buch)
Herder Verlag Freiburg-Basel-Wien: Herders Neues Volkslexikon,
5.Auflage 1976
Hinner, Kajetan: Lexikon der
Telekommunikation
Kosmos electronic X3000-X4000- Experimentierbuch für die Grundkästen
X3000 und X4000, Franckh'sche Verlagshaltung W. Keller & Co. Stuttgart,
4.Auflage 1989
Paetec Verlag: Duden Technik, Basiswissen Schule (CD-Rom)
Samal, E.: Grundriß der
praktischen Regelungstechnik, Ouldenbourg Verlag, 17.Auflage
Stam-Verlag Köln München: Elektrotechnische Schaltungen und ihre
Funktion, 10.Auflage
Weißgerber, Wilfried: Elektrotechnik für Ingenieure Band 1-3, Vieweg Verlag, 3., korrigierte
Auflage 1996
Zander, Horst: Datenwandler A/D-
und D/A- Wandler, Vogel Buchverlag, 2. Auflage 1990
Internetquellen:
chemieonline.de/forum/archive/index.php/t-1121.html
emvgmbh.de/03_b_emv_messtech/PDF_Wissen/FA_HF_BreitbandleistVerst.pdf
networks.siemens.de/solutionprovider/
elektronik-kompendium.de/sites/kom/0401251.htm
iva.uni-ulm.de/PHYSIK/VORLESUNG/ELEHRE/node131.html
Erklärung:
"Ich erkläre, dass ich die Facharbeit ohne fremde Hilfe angefertigt und
nur die im
Literaturverzeichnis angeführten Quellen und Hilfsmittel benutzt
habe."








