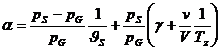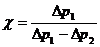Referat Gase und Dämpfe - Bestimmung des Spannungskoeffizienten

Grundpraktikum II

Gase und Dämpfe

Bestimmung des Spannungskoeffizienten

Das Gasthermometer dient in unserem Fall zur Ermittlung des Spannungskoeffizienten von Luft, die als ideales Gas angesehen wird. Beim Gasthermometer wird eine Temperaturmessung auf eine Druckmessung zurückgeführt. Es besteht aus einem Rezipienten , welcher über eine Kapillare B mit dem Quecksilberthermometer zwei beweglichen Schenkeln verbunden ist. Im linken Schenkel befindet sich ein kleiner Metalldorn, dessen Spitze als Nullmarke für den linken Quecksilbermeniskus dient. Abgelesen werden an einer Spiegelskala h_r und h₁, woraus die Höhendifferenz gebildet wird.

Um den Spannungskoeffizienten zu bestimmen, wird der Rezipient zunächst in ein Eisbad und dann in ein Bad aus siedendem Wasser getaucht.

Abgelesen wird dabei jeweils der Höhenunterschied der Quecksilbersäule. Der gesamte Luftdruck ergibt sich dann aus dem Druck, der aus dem Höhenunterschied berechnet werden kann, sowie dem barometrischen Luftdruck b.

Als Einheit wird hier Torr verwendet. Das hat den Vorteil, dass der Höhenunterschied, der ja die Einheit mm Quecksilbersäule hat, direkt als Druck hergenommen werden kann. Die Einheit des Luftdruckes kann am Labormessgerät ebenfalls in Torr abgelesen werden.

Zuerst wurde der barometrische Luftdruck im Praktikumsraum bestimmt. Das Heberbarometer lieferte uns folgenden Wert für den Luftdruck:

b = 733 Torr

Die Einheit Torr stellt sich hier als sehr praktisch heraus, da beim Ablesen des Druckes am Gasthermometer die Einheit mm Quecksilbersäule abgenommen wird, was ja identisch mit der Einheit Torr ist.

Folgende Tabelle zeigt die gemessenen Werte des Druckes in Torr (mm Hg-Säule) sowie die errechneten Gesamtdrücke unter Berücksichtigung des Luftdruckes:

h_l=81,3 cm h_r=78,2 cm Dh_G = -31 mmHg p_G = 702 Torr

h_l=81,45 cm h_r=102,8 cm Dh_S = 213,5 mmHg p_S = 946,5 Torr

Die Siedetemperatur des Wassers liegt laut Walcher Tab. A3.1 Seite 399 für einen barometrischen Druck von 733 Torr bei ca. 99°C.

J_S = 99°C

Daraus lässt sich nun der Spannungskoeffizient bestimmen:

Zwischen den Drücken, die sich beim Eisbad bzw. beim Bad aus siedendem Wasser einstellen, besteht folgender Zusammenhang:

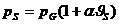
daraus lässt sich nun unsere gewünschte Größe berechnen:

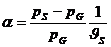
a = 0,000931 K^-1

Für ideale Gase gilt:

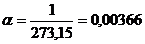K^-1

Die Abweichung zwischen den beiden Werten beträgt ÜBER 400%

Obige Formel gilt allerdings nur dann, wenn sich das gesamte Luftvolumen auf gleicher Temperatur befindet. Dies ist bei uns allerdings nicht der Fall, da sich in der Kapillare B und im Bereich des Dorns

Luft mit Zimmertemperatur befindet.

Tz = 296,8 K

Der thermische Ausdehnungskoeffizient beträgt für AR-Glas:       g = 276.10^-7 K^-1

Laut Werkstattzeichnung ergeben sich für die beiden Volumina:

V = 157806 mm³

v = 3447,64 mm³

Zu beachten ist weiters, dass sich das Glas des Gasthermometers abhängig von der Temperatur ausdehnt.  Mit Hilfe des Ansatzes, dass die eingeschlossene Stoffmenge konstant bleibt, erhält man für den Spannungskoeffizienten a in besserer Näherung:

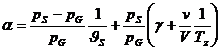
a Spannungskoeffizient von Luft

Jb Siedetemperatur des Wassers, abhängig vom barometrischen Druck

p_G Druck, der sich beim Abkühlen auf 0°C einstellt

p_S Druck, der sich beim Erwärmen auf Siedetemperatur einstellt

g thermischer Ausdehnungskoeffizient des Glasgefäßes

v Volumen des schädlichen Raumes, totes Volumen

V Volumen des Rezipienten (A)

T_z thermodynamische Zimmertemperatur

Die thermodynamische Zimmertemperatur wird bestimmt, indem man zuerst den Druck bei Zimmertemperatur misst und mit Hilfe des Druckes, der sich beim Eisbad einstellt, unter Anwendung des Gasgesetzes die Temperatur berechnet.

Es gilt folgender Zusammenhang:

Bestimmung des Adiabatenexponenten

Mit Hilfe dieses Versuches lässt sich der Adiabatenexponent bestimmen. Man verwendet ein Gefäß mit angeschlossenem U-Manometer und Dreiwegehahn, mit dem der Rezipient abgesperrt oder mit einem Blasebalg verbunden werden kann. Eine Verbindung mit der Außenluft wird bei unserem Versuch dadurch erreicht, dass ein Gummistopfen aus dem Tubus gezogen wird.

Das U-Manometer  ist mit Silicon- oder Paraffinöl gefüllt.

Nachstehendes Bild zeigt den Versuchsaufbau:

Das Verfahren arbeitet in 4 Phasen:

Mit Hilfe des Blasebalges wird ein Überdruck von ca. 100mm Ölsäule erzeugt. Seien nun b der Barometerdruck und T₀ die thermodynamische Anfangstemperatur (Zimmertemperatur). Die Zustandsgrößen der in A eingeschlossenen Luftmenge sind:

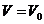
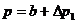
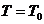
Man verbindet durch Herausziehen des Gummistopfens den Rezipienten mit der Außenluft. Hierdurch erfolgt Druckausgleich. Das Gas expandiert und verrichtet dabei Arbeit gegen den äußeren atmosphärischen Druck. Diese Arbeit wird auf Kosten der "inneren" Energie des Gases A verrichtet, die Temperatur des Gases sinkt. Die Zustandsgrößen der in 1. betrachteten Gasmenge sind nunmehr:

             

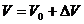
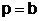
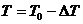
Sofort nach erfolgtem Druckausgleich sperrt man das Gefäß wieder ab. Zustandsgrößen:

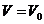
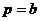
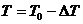
Durch Wärmeaustausch mit der Umgebung nimmt die Luft in A im Laufe von etwa 10 Sekunden wieder ihre Anfangstemperatur an. Diese Zustandsänderung erfolgt isochor. Der Druck steigt dabei um Dp₂ an, sodass sich folgender Zustand einstellt

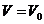
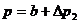
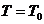
Wegen der Schnelligkeit der Zustandsänderung 1 auf 2 kann angenommen werden, dass kein Wärmeaustausch mit der Umgebung stattfindet, der Prozess kann also als adiabatisch angesehen werden. Die ersten beiden Zustände sind miteinander durch die Poissonschen Zustandsgleichungen verknüpft:

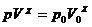oder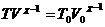

Die Zustandsgrößen aus 3. und 4. Sind durch die Zustandsgleichungen idealer Gase miteinander Verknüpft:

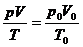
Unter Berücksichtigung, dass DV << V und Dp₁ << b ergibt sich als einfache Endformel:

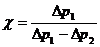
Unten stehende Tabelle zeigt die fünf durchgeführten Messreihen und die daraus errechneten Adiabatenexponenten:

Der Mittelwert des Adiabatenexponenten beträgt 1,29907, die Standardabweichung 0,0394.

Der genaue Wert für dreiatomige Gase beträgt 1,33. Da Luft aber keineswegs als ein, zwei- oder dreiatomiges Gas angesehen werden kann, ist die Abweichung durchaus vertretbar.

Bestimmung der Luftfeuchtigkeit

Das Schleuderpsychrometer dient zur Messung der Luftfeuchtigkeit nach dem nachfolgenden Messprinzip: ein trockenes Thermometer misst die Umgebungstemperatur, ein weiters Thermometer ist mit einem Doch umgeben, welcher mit destilliertem Wasser befeuchtet wird. Beim Rotieren des Schleuderpsychrometers verdunstet ein Teil des Wassers im Docht und kühlt dabei das entsprechende Thermometer bis zum Taupunkt ab.

Der Taupunkt ist jene Temperatur , bei der die maximale absolute Luftfeuchtigkeit erreicht wird. Bei Temperaturen über dem Taupunkt ist der Dampf ungesättigt, bei Temperaturen darunter ist der Dampf übersättigt und kondensiert.

Am Taupunkt wird dem Docht genauso viel Feuchtigkeit entzogen wie aus der Umgebung zugeführt, die Temperatur bleibt daher stabil.

Aus dieser Temperatur lässt sich im Prinzip die absolute Feuchte aus der Dampfdruckkurve des Wassers bestimmen.

Es gilt:

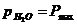
Wird das Psychrometer mit mindestens 3 U/s gedreht, ist der thermische Verlust des Psychrometers berechenbar:

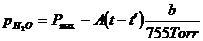
p_H2O aktueller Dampfdruck des Wassers

P_max der bei gegebener Temperatur maximal mögliche Dampfdruck

A Psychrometerkonstante

t Temperatur des trockenen Thermometers

t' Temperatur des feuchten Thermometers

b Luftdruck

Daraus lässt sich nun die aussagekräftige Größe der relativen Luftfeuchtigkeit bestimmen:

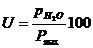
Folgende Messdaten wurden bei diesem Versuch aufgenommen:

Messung im Labor: t = 23,6 °C P_max = 21,8 Torr

t' = 12,8 °C

Datum: 27.03.01                    Uhrzeit: 15:48

Messung im Freien: t = 5,0 °C P_max = 6,6 Torr

t' = 2,4 °C

Datum: 27.03.01                    Uhrzeit: 15:57

Der maximal mögliche Dampfdruck bei der jeweiligen Temperatur wurde der Tabelle A3.1, Walcher Seite 399 entnommen.

In der Tabelle auf der nächsten Seite sind nun die errechneten Werte aufgestellt. Die sehr hohe Luftfeuchtigkeit im Freien ist durchaus möglich, da es zum Zeitpunkt der Messung nebelig war und es kurz darauf zum Regnen angefangen hat.

Zur exakten Berechnung wurde für die Psychrometerkonstante ein Wert von 0,0006623 Pa/K angenommen. Der Luftdruck wurde aus dem 1. Versuch übernommen.