Referat Welleneigenschaften mit Mikrowellen

Welleneigenschaften mit Mikrowellen

Mikrowellen sind ebenfalls el.mag. Wellen mit Wellenlängen im cm-Bereich und f im Gigahertz-Bereich .

I.      Strahlenförmige Mikrowellen (Sendecharakteristik)

Reflexion an einer Metallwand

a)      Welle trifft senkrecht auf Metallplatte : Interferenz : stehende Welle : Abstand zwischen 6 Knoten ( 5*l /2) : 8 cm (nicht von Wand aus messen) : Wellenlänge = 3,2 cm : bei Sende-f von 9,35 GHz : c = l *f = 3*10⁸ m/s .

b)      Welle trifft unter Winkel α auf Platte : wird unter Winkel α reflektiert : Reflexionsgesetz (Einfallswinkel = Reflexionswinkel) gilt auch bei el.mag. Wellen .

Polarisationsebene (Welle auf Gitter)

Linear polarisierte Welle trifft (senkrecht) auf Metallgitter :

a)      Gitterstäbe sind parallel zu E (= vertikal) : Empfänger registriert hinter Gitter kein Signal mehr , vor Gitter aber steh. Welle .

b)      Gitterstäbe senkrecht zu E : registriert weiterhin Signal .

c)      Gitterstäbe um 0°< α < 90° gegenüber Polarisationsebene gedreht : entsprechend schwächerer Empfang .

Erklärungen

Parallel zu E stehenden Gitterstäbe = Hertzsche Dipole : Eigen-f   f _G << Sende-f f _S da ihre Länge D erheblich größer als ausgestrahlte Wellenlänge ist : Oberschwingungen werden angeregt : Bed. D = k*l /2 automatisch erfüllt : für hohe k verteilt sich Fehler zwischen l _{Reson anz} und l auf viele Wellenlängen : l (und damit f) liegt immer noch im Resonanzbereich . Schwingungen zu denen Gitterstäbe angeregt wurden sind um nahezu 180° gegenüber anregender Schwingung phasenverschoben (vgl. erzw. Schwing.) . Welle _Gitter in Empfängerrichtung löscht ursprüngliche Welle aus , in Sendedipolrichtung Interferenz mit ursprünglicher Welle : steh. Welle . 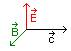Metallwand ist auf Gitter mit sehr nahen Stäben : Reflexion . An Wand E-Knoten und B-Bauch , E macht Phasensprung von 180° , B ohne Phasensprung reflektiert , bilden immer folgendes Dreibein :

Steht Gitter verdreht : Abschwächung Empfang : Zerlegung der einfallenden Welle in Komponente parallel (Reflexion) zu Gitterstäben und Komponente senkrecht (Durchlass) dazu . Wenn Empfangsdiode ebenfalls gedreht wird (senkrecht zu gedrehten Gitterstäben steht) : max. Signal .

Beugung am Spalt

Brechung

Übergang : Luft - Sand

sin α/sin β = c ₀ /c _Sand = √ ε _r

Def.: sin α/sin β = c ₀ /c _Medium = n heißt Brechzahl des Mediums , Gleichung heißt Brechungsgesetz . Es gilt c ₀ /c _Medium = √ ε _r = n .

Allg.: Beim Übergang von Medium 1 nach Medium 2 gilt :

sin α ₁ /sin β ₂ = c ₁ /c ₂ = √(ε _{r, 2} /ε _r,1) = n ₂ /n ₁

Huygens'sches Prinzip

1. Punktförmiger Erreger  2. Geradliniger Erreger

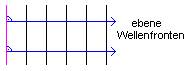
Def.: Wellenbeschreibung mittels Wellenfronten oder gleichwertig mittels Wellenstrahlen . Welle trifft auf Spalt : Hinter Spalt entsteht Elementarwelle : Spalt verhält sich wie punktförmiger Wellenerreger .

Huygens : 1. Jeder Pkt einer Wellenfront kann als Ausgangspkt einer

Elementarwelle angesehen werden .

2. Jede Wellenfront ist die Einhüllende von Elementarwellen .

Anwendungen des Huygens'schen Prinzips

1. Wellenausbreitung

2. Beugung am Spalt

Der Spalt ist Ausgangspkt einer Elementarwelle , da es keine weiteren Ausgangspkte gibt , ist diese gleichzeitig die (auch beobachtete) Wellenfront .

3. Reflexion

4. Brechung

Optik

Brechung bei Licht

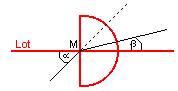
Lichtstrahl trifft auf halbzylinderförmigen Plexiglaskörper . Beim Messen des Einfallswinkels α und Ausfallwinkels β zeigt sich : Brechungsgesetz gilt für Licht :

Lichtgeschwindigkeit

Ausbreitungsgeschwindigkeit in Medien

5 cm dicker Plexiglaskörper wird in den Lichtweg gebracht : in Plexiglas Ausbreitungsgeschwindigkeit kleiner : Verschiebung des Oszi-Bildes : Licht braucht länger : ≈ 10 mm 52 ns / 600 = Δt = t _Glas - t _Luft = 8,7*10^-11 s (Wobei t _Luft = Zeit die Licht für a = 5 cm in Luft benötigt und t _Glas = Zeit die Licht für a in Glas benötigt) : Δt = t _Glas - t _Luft = a/c _Glas - a/c ₀ : c _Glas = c ₀*a/(a+ c ₀ Δt) = 2,0*10⁸ m/s : n _Glas = c ₀ /c _Glas = 1,5 .

Wiederholung obigen Versuchs mit Wasser :

Daten : a = 1 m ; Δt = 6,6*10^-7 s/600 = 1,1*10^-9 s :

c _w = c ₀ *a/(a+ c ₀ Δt) = 2,3*10⁸ m/s   : n _w = c ₀ /c _w = 1,3 .

Interferenz bei Licht

Abstand des k-ten Max. vom k+1-ten (benachbarte Max. , α klein) : Δd = d _{k +1} -d _k = (k+1) l* a / g - k* l* a/g = l* a(k+1-k)/g = l* a/g . Anzahl der Max (! Keine kleinen Winkel α) : d ≤ g T   k* l ≤ g .