Verkehrstheorie
Allgemeines
Definition
der Verkehrstheorie
Annahmen
der Verkehrstheorie
Begriffe
des Fernsprechverkehrs
Charakteristische
Verkehrsgrößen und Definitionen
Eigenschaften
des Fernsprechverkehrs
Verlustsystem
Systeme
mit vollkommener Erreichbarkeit
Systeme
mit begrenzter Erreichbarkeit
Wartesysteme
Wartesysteme
ohne Prioritäten
Wartesysteme
mit nichtunterbrechenden Prioritäten
Weitere
Systeme mit Wartemöglichkeit
Verkehrsmessungen
Messungen
von Parametern
Ermittlung
von Verteilungsfunktionen
Umfang
der Messungen
Durchführung
der Messungen
Weitere
Anwendungen der Verkehrstheorie
Quellenangaben
Allgemeines
Definition
der Verkehrstheorie
Die Verkehrstheorie ist ein mathematische Beschreibung
statistischer Vorgänge und dient zum geeigneten Dimensionieren von
Datenverkehrseinrichtungen (Koppelnetzwerke, Leitungen), da jeder
Verkehrsteilnehmer zu jeder Zeit ohne spürbare Wartezeiten Verbindungen
herstellen möchte, die Betreiber der entsprechenden Anlage (Fernsprechanlage,
Datenverarbeitungsanlage, usw.) wiederum möchten kostengünstig alle
Verbindungswünsche mit ausreichender Übertragungsqualität zufriedenstellen.
Der Begründer der Verkehrstheorie war A.K.
Erlang (1878-1927).
Das Hauptanwendungsgebiet der Verkehrstheorie
war und ist der Fernsprechverkehr. Hierfür beschäftigt sie sich mit folgenden
Problemen:
zu welcher Zeit und wie oft
Fernsprechteilnehmer Gespräche aufbauen
wie lange sie sprechen und dadurch
Vermittlungseinrichtungen beanspruchen
Die Ergebnisse, die man mit Hilfe der
Verkehrstheorie erhält, sind Formeln, Rechenregeln, Tabellen u. ä.
Beispiel zur Erläuterung der Problematik
der Verkehrstheorie:
Wohnhausanlage mit 20 Wohnungen und ebenso
vielen Telefonanschlüssen:
Angenommen es gibt so viele Telefonleitungen wie Teilnehmer zur
nächsten Fernsprechvermittlungsstelle, d.h. um eine 100% Auslastung zu erzielen
müßte jeder Teilnehmer 24 Stunden pro Tag, sein ganzes Leben lang telefonieren.
Da dies auf äußerst wenige Menschen zutrifft (im Schnitt werden 10 - 60 min in
24 Std. pro Teilnehmer gerechnet), ist diese Überlegung als eindeutig
unwirtschaftlich einzustufen.
Angenommen es gäbe nur eine Leitung von dieser Wohnhausanlage zur
Vermittlungsstelle, so wäre diese eindeutig überlastet. Zwar würden rein
mathematisch betrachtet für jeden Teilnehmer mehr als 60 min. zur Verfügung
stehen, aber die Wahrscheinlichkeit ist äußerst groß, daß zu gewissen
Tageszeiten ein erhöhtes Anrufbedürfnis herrscht. Somit wäre zu gewissen Zeiten
die Leitung ständig besetzt und der Kunde äußerst unzufrieden.
FAZIT: Die Zahl der Leitungen muß in diesem
Fall zwischen 1 und 20 liegen. Um die genaue Anzahl zu ermitteln müssen
verschiedene Annahmen getroffen und diverse Begriffe geklärt werden.
Annahmen
der Verkehrstheorie
A. Telefonanschlüsse werden nicht voll ausgenützt. Angenommenes Mittel pro
Teilnehmer: 10 - 60 min. /24 Std.
B. Die von den Teilnehmern erzeugten Verbindungswünsche entstehen rein
zufällig.
C. Die Nichtlinearität der Verbindungswünsche in Abhängigkeit der
Tageszeit, des Wochentages und der Jahreszeit, d.h. die Verkehrsintensität wird
in der Silvesternacht wesentlich höher sein als an einem x-beliebigen Tag im
Jahr um 3 Uhr morgens.
Begriffe
des Fernsprechverkehrs
Koppelpunkte (KP):
Schaltmittel, die es ermöglichen, eine
Verbindung zwischen zwei Leitungen herzustellen und wieder zu trennen, nennt
man Koppelpunkte. Da pro Kommunikationseinrichtung meist zwei Adern für die
Signalübertragung verwendet werden, hat man pro Koppelpunkt zwei Kontakte, die
gleichzeitig betätigt werden, um eine Verbindung durchzuschalten oder zu
trennen.
Koppelanordnung (KA):
Einrichtungen, die ein Durchschalten von
Verbindungen zwischen mehreren Teilnehmern oder Leitungen ermöglichen, nennt
man Koppelanordnungen.
Koppelreihe (KR):
Eine Reihe aus Koppelpunkten, mit denen man
eine Leitung wahlweise mit mehreren Leitungen verbinden kann, nennt man eine
Koppelreihe.
Beispiel
Koppelreihe mit einem Eingang und k Ausgängen
Koppelvielfach (KV) bzw. Koppelmatrix:
Mehrere Koppelpunkte, die so geschaltet sind,
daß jede an die "i"-Seite angeschlossene Leitung jede Leitung an der "k"-Seite
erreichen kann.
Charakteristische
Verkehrsgrößen und Definitionen
Hauptverkehrsstunde (HVStd):
Die Verkehrsintensität schwankt durch das
Verhalten der Fernsprechteilnehmer je nach Tageszeit, Wochentag und Jahreszeit.
In der abgebildeten Kurve erkennt man unterschiedliche Einflüsse, z.B.
Beginn und Ende der Arbeits- und
Geschäftszeiten
Mittagspausen
Beginn des ermäßigten Tarifs und
Eintritt der Nachtruhe

Teilnehmerverhalten
Es wäre unwirtschaftlich, die Vermittlungsanlagen
in einem Netz so auszubauen, daß auch die größten Verkehrsspitzen restlos
bewältigt werden. Andererseits wäre es den Teilnehmern gegenüber unzumutbar,
wenn die Anlagen nur einer mittleren Verkehrsintensität des Tagesverlaufs
gewachsen wären. Deshalb ermittelt man eine für eine Anlage repräsentative
Stunde, deren Verkehrsintensität für den Ausbau der Anlage maßgebend sein soll.
Diese Hauptverkehrsstunde wird ermittelt, indem an mehreren
aufeinanderfolgenden Tagen (5 bis 10 Werktagen) viertelstündlich der Verkehr
gemessen wird. Jeweils vier aufeinanderfolgende Meßwerte werden zusammengefaßt
und zur Mittelwertbildung über alle Meßtage verwendet. Die Hauptverkehrsstunde
hat also keine bestimmte zeitliche Lage. Ermittelt wird auf diese Weise eine
mittlere Belastung während einer gedachten Hauptverkehrsstunde. Im allgemeinen
gelten die Angaben der Verkehrstheorie für die Hauptverkehrsstunde.
cy:
tatsächlich zustande gekommene Belegung; gibt
an wie viele Verbindungen innerhalb einer gewissen Zeit zustandegekommen sind;
[cy] = 1/s
ca:
angebotene Belegungswünsche; gibt an wie viele
Verbindungen innerhalb einer gewissen Zeit möglich gewesen wären; [ca]
= 1/s
cv:
verlorengegangene Belegungswünsche; gibt an
wie viele Verbindungen innerhalb einer gewissen Zeit nicht zustandegekommen
sind; [cv] = 1/s
tm:
mittlere Belegungsdauer; gibt an, wie lange
eine Verbindung im Schnitt dauert; [tm] = s
Verkehrswert (Belastung) Y:
Der über Koppelanordnungen durchgeschaltete
Verkehr
 Belegungen
(c) in einem bestimmten Zeitraum * mittl. Belegungsdauer (tm)
Belegungen
(c) in einem bestimmten Zeitraum * mittl. Belegungsdauer (tm)
[Y] = Erlang (Erl) künstliche Einheit
Die Einheit des Verkehrs 1 Erl könnte man auch
so definieren, daß eine Einrichtung oder Leitung in einer Stunde 60 Minuten
lang durch Belegungen genutzt ist. Dabei stellt 1 Erl den Höchstwert dar, der
nur unter idealen Bedingungen erreicht werden kann. Hierzu einige Beispiele:
Eine Leitung kann einen
Verkehrswert von 1 Erl erbringen.
Ein PCM-Kanal hat ebenfalls max. 1
Erl.
Ein PCM-Highway hat also max. 30
Erl (weil 30 Kanäle verfügbar)
Durchschnittliche Verkehrswerte:
Teilnehmeranschluß an
Nebenstellenanlagen Y = 0.2 Erl
Teilnehmeranschluß am öffentlichen
Netz 0.1 bis 0.15 Erl
Leitungen zwischen
Nebenstellenanlagen und OVSt 0.8 Erl
Verkehrsangebot A:
 der von den
Quellen (Teilnehmern) angebotene Verkehr
der von den
Quellen (Teilnehmern) angebotene Verkehr
Verkehrsrest R:
Geht bei Verlustsystemen verloren und wird bei
Wartesystemen eingereiht.

Verlust:
Wahrscheinlichkeit, daß ein Belegungswunsch
verloren geht.
 V ist
bezogen auf die geleisteten Belegungen
V ist
bezogen auf die geleisteten Belegungen
 B ist
bezogen auf die angebotene Belegung
B ist
bezogen auf die angebotene Belegung 
allgemeine Wahrscheinlichkeitsverteilung
F(t)
Anzahl der Quellen q
Eigenschaften
des Fernsprechverkehrs
Betrachtet man eine einzige Leitung, so stellt
man unterschiedliche Belegungs- und Pausenzeiten fest. Eine gute Näherung für
die Wahrscheinlichkeitsverteilung F(t), der von den Teilnehmern verursachten
Belegungsdauer, ist die negativ exponentielle Verteilung.

e Enderate (Wahrscheinlichkeitsdichte
für das Enden einer Belegung) 
tm mittlere Belegungsdauer
(einige Minuten)
F(t) ist hier die Wahrscheinlichkeit, daß die
Dauer einer Belegung größer als die Zeit t ist (z.B. die Wahrscheinlichkeit,
daß ein Telefongespräch länger 3tm dauert ist ca. 5%).
Entsprechend analog können auch die Quellen
betrachtet werden. Die neg. exponentielle Verteilung ist auch für die
Pausenzeiten der freien Quelle eine gute Näherung. Mit der mittleren Pausenzeit
einer Quelle (am) erhält man die Wahrscheinlichkeitsdichte für das
Enden einer Pausenzeit = Wahrscheinlichkeitsdichte für das Eintreffen eines von
dieser Quelle herrührenden Anrufs (Anrufrate).
a Anrufrate 
am mittlere Pausenzeit einer
Quelle
Wahrscheinlichkeitsverteilung der
Anrufabstände: 
In der Praxis interessiert man sich nicht für
eine Quelle oder Leitung; sonder für ein Bündel von Leitungen; man beschäftigt
sich mit der Frage, wieviel Leitungen zu irgendeinem Zeitpunkt belegt sind. Da
fortlaufend neue Belegungen hinzukommen und andere enden, ergibt sich das unten
dargestellte Belegungsgebirge und die Wahrscheinlichkeitsverteilung für dieses
Beispiel.
Von besonderer Bedeutung sind jene Zeiten, in
denen alle Leitungen belegt sind. Erhält ein Bündel mit 4 Leitungen von mehr
als 4 Quellen Belegungswünsche, so unterscheidet man verschiedene Systeme:
Im Verlustsystem werden die
Belegungswünsche, die eintreffen während alle n Leitungen belegt sind,
abgewiesen (sie gehen verloren). Der Teilnehmer hört den Besetztton. Unser
Fernsprechsystem ist ein Verlustsystem.
Im Wartesystem werden, falls alle n
Leitungen belegt sind, die Belegungswünsche so lange gespeichert, bis eine
bestehende Belegung. Für die Zahl der Warteplätze s gilt: s q - n
Im Warte-Verlustsystem ist die Anzahl
der Warteplätze s begrenzt: s < q - n . Dadurch werden zwar die
Belegungswünsche gespeichert falls alle n Leitungen belegt sind, doch wenn alle
Warteplätze belegt sind, werden eintreffende Belegungswünsche abgewiesen und
gehen somit verloren.
Verlustsystem
Systeme
mit vollkommener Erreichbarkeit
Die Erlangsche Verlustformel:
Ausgehend von einem System mit vollkommener
Erreichbarkeit (d.h. jede Quelle kann mit jeder freien Leitung verbunden
werden; jede Zubringerleitung kann jede Abnehmerleitung erreichen), wird die
Verteilungsfunktion P(x) für die Bündelbelegung hergeleitet. Für diesen Zweck
geht man von "x belegten Leitungen" aus: 0 £ x n
Es gilt:
Wahrscheinlichkeitsdichte
für das Verlassen des Zustandes "x Leitungen belegt" =
Wahrscheinlichkeits-dichte für das Entstehen des Zustandes "x Leitungen belegt"
aus allen Nachbarzuständen.
Die "Zustandsübergänge" werden durch
neue Belegungswünsche bzw. durch Gesprächsbeendigungen verursacht. D.h.: Sind
beispielsweise 4 Leitungen belegt, so geht dieser Zustand in den Nachbarzustand
von 3 Leitungen (bei Gesprächsbeendigung), bzw. von 5 Leitungen (bei neuem
Belegungswunsch) über.
lx Übergangsrate
herrührend von eintreffenden Anrufen  (Quellen minus
belegten Leitungen mal Anrufrate)
(Quellen minus
belegten Leitungen mal Anrufrate)
ex
Übergangsrate herrührend von endenden Belegungen  (Enderate mal belegten
Leitungen bzw. belegte Leitungen durch mittlere Belegungsdauer)
(Enderate mal belegten
Leitungen bzw. belegte Leitungen durch mittlere Belegungsdauer)
Ansatz für die Erlangsche Verlustformel:

In Worten bedeutet diese Formel:
UND ist
gleich ODER
Diese Formel ist die Rekursionsformel für die
Zustandswahrscheinlichkeit P(x) (rekursiv zurückgehend auf bekannte Werte).
Wir werden in den folgenden Schritten
versuchen aus obigem Ansatz P(x) auszurechnen, die Wahrscheinlichkeit, daß x
Leitungen belegt sind.
Dafür setzen wir in die Formel für x=0 ein:


Die Wahrscheinlichkeit, daß einer auflegt wenn
keiner telefoniert ist 0 ( )
)
Die Wahrscheinlichkeit, daß minus eine Leitung
belegt ist, ist ebenfalls 0.

Für x=1 (wieder in Rekursionsformel
eingesetzt):

Durch Ersetzen von P(1) durch P(0) erhält man:

Wenn man jetzt für x = 2, 3, 4, einsetzen
würde erhält man eine allgemeine Formel:

Da immer irgendeine Anzahl von Leitungen
belegt ist gilt:
 bzw.
bzw. 
Setzt man nun für P(x) in dieser Formel ein,
kann man sich P(0) ausdrücken und in der Formel für P(x) rückeinsetzen. Man
erhält dann für P(x):

Durch Einsetzen von und
und  erhält man die
gesuchte Verteilungsfunktion für die Bündelbelegung:
erhält man die
gesuchte Verteilungsfunktion für die Bündelbelegung:
 ERLANG'S BERNOULLI
FORMEL
ERLANG'S BERNOULLI
FORMEL
Zufallsverkehr 2.Art (Engseth -
Charakter)
Für die folgenden Formeln wird von einer
überschaubaren Quellenanzahl q und erfaßbaren Anrufraten a ausgegangen:
Belastung Y des Bündels: 
Angebot A:  weil
weil 
aus obigen Formeln erhält man auch:  da
da 
Verkehrsrest R (Angebot bei x = n): 
prozentueller Verlust B: 
Die Belastung Y läßt sich auch, um die
Summation zu umgehen, über A und R ausdrücken:
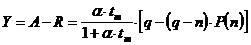
Zufallsverkehr 1.Art (Erlang -
Charakter)
Durch das bestehende Telefonnetzwerk ist die
Zahl der Quellen extrem hoch (q® ), die Anrufrate je freier Quelle hingegen extrem gering (a 0). Somit ist der Grenzwert der Anrufrate l konstant.

Für das Angebot A gilt somit: 
Daraus ergibt sich die Erlangsche Verteilung
P(x), bzw. die Erlangsche Verlustformel, welche aus dem auftretenden Verlust
resultiert (für x=n, wenn alle n Leitungen belegt sind).


Da es sich hier um statistische Werte handelt,
wurden diese bereits berechnet und in Tabellen festgelegt, welche in der Praxis
benutzt werden.
Die Verlustwahrscheinlichkeit B kann auch in
folgendem Diagramm abgelesen werden:
Verlustwahrscheinlichkeit
B als Funktion des auf die Anzahl n der Abnehmer bezogenen Angebots A bei
vollkommener Erreichbarkeit und Zufallsverkehr 1.Art für verschiedene n
Systeme
mit begrenzter Erreichbarkeit
Hier werden im Gegensatz zu k = n (2.1.
Systeme mit vollkommener Erreichbarkeit) Koppelanordnungen mit begrenzter
Erreichbarkeit behandelt: k < n
Begrenzte Erreichbarkeit hat eine Einrichtung,
wenn Zubringerleitungen nur einen Teil der Abnehmerleitungen erreichen können.
k Anzahl der Koppelanordnungen
Im System mit begrenzter Erreichbarkeit kann
nicht jede Quelle mit jeder freien Leitung verbunden werden. Trotzdem gibt es
für den Einsatz dieses Systems mehrere Gründe:
Konstruktive Beschränkungen für die Größe der Koppelvielfache
Teure Koppelpunkte fallen weg
Fehlende Zeit zum Absuchen des ganzen Abnehmerbündels
Wartesysteme
Im Gegensatz zum Verlustsystem, bei dem die
Belegungswünsche verloren gehen, wenn die Verbindung belegt ist, werden sie
beim Wartesystem in eine Warteschlange eingereiht. Diese muß so dimensioniert
sein, daß alle zusätzlichen Wünsche in ihr Platz finden (hat die Warteschlange
nicht genug Platz, dann gehen alle Belegungswünsche, die nach totaler Belegung
der Warteschlange eintreffen verloren. In diesem Fall spricht man von einem
Warte-Verlust-System).
Wartesysteme müssen bei Systemen zum Einsatz
kommen, wo keinerlei Verluste auftreten dürfen, wie z.B. bei
Paketvermittlungssystemen oder Datenverarbeitungsanlagen.
Maßgebend für die Beurteilung eines
Wartesystems ist die Wahrscheinlichkeit dafür, daß ein Anruf länger als eine
Zeit t warten muß, d.h. die Überschreitungswahrscheinlichkeit P(>t),
speziell die Wahrscheinlichkeit P(>0) dafür, daß ein Anruf überhaupt warten
muß, und entweder die mittlere Wartezeit aller Anrufe tw*
oder die mittlere Wartezeit nur der wartenden Anrufe tw.
Beide sind durch

verknüpft, da sich die mittlere Wartezeit
aller Anrufe anteilig aus der der wartenden und der der nicht wartenden Anrufe
zusammensetzt.
Für die Bemessung der Warteschlangen ist die
Anzahl der wartenden Anrufe maßgebend. Ihr Mittelwert w, der allein zur
Bemessung natürlich nicht ausreicht, ergibt sich aus der mittleren Anzahl der
pro Zeiteinheit eintreffenden Anrufe A/tm und der mittleren
Wartezeit aller Anrufe, sofern alle Anrufe beliebig lange warten können, sofern
also weder die Wartezeit noch die Warteschlange in ihrer Länge begrenzt sind:

Diese Beziehung gilt in dieser Form für die
Gesamtheit aller Anrufe; werden Prioritäten verwendet, dann gelten
entsprechende Beziehungen je Priorität j:

Im folgenden wird im allgemeinen davon
ausgegangen, daß das Angebot zustandsunabhängig ist (q® ) und die Anrufabstände negativ exponentiell verteilt sind. Zuerst
werden Anordnungen mit n Abnehmern betrachtet, dann solche mit nur einem
Abnehmer. Sie spielen bei Wartesystemen große Rolle, da der Zugriff zu
zentralen Vermittlungseinrichtungen im allgemeinen über ein Wartesystem
erfolgt. Aus dem gleichen Grund ist es hier von besonderer Bedeutung, auch den
Fall konstanter Belegungsdauern zu berücksichtigen. Dagegen werden Wartesysteme
mit begrenzter Erreichbarkeit hier außer Acht gelassen, d.h. es wird im
folgenden stets vollkommene Erreichbarkeit vorrausgesetzt.
Wartesysteme
ohne Prioritäten
Entsprechend dem Vorgehen bei der Darstellung
von Verlustsystemen soll hier ein System mit mehreren Abnehmern betrachtet
werden, dem Zufallsverkehr angeboten wird. Es gebe nur eine einzige
Warteschlange und keine Prioritäten. Die Warteschlange sei unbegrenzt, ebenso
die Wartezeit, und die Anrufe werden in der Reihenfolge ihres Eintreffens abgefertigt.
Ein stationärer Prozeß ist nur dann vorhanden, wenn im Mittel weniger Anrufe
eintreffen als durch die n Abnehmer überhaupt verarbeitet werden können, d.h. A
muß kleiner als n sein.
Die Wartewahrscheinlichkeit ergibt sich aus
der Wahrscheinlichkeit dafür, daß ein Anruf eintrifft und warten muß, bezogen
auf die Wartewahrscheinlichkeit dafür, daß - im gleichen Zeitabschnitt - überhaupt ein Anruf eintrifft. Bei Zufallsverkehr 1.Art erhält man,
abgeleitet aus den Zustandswahrscheinlichkeiten,
 ,
,
also eine ähnliche Beziehung wie die
Erlangsche Verlustformel. Die Wahrscheinlichkeit dafür, daß alle n Abnehmer
belegt sind und mehr als r Anrufe warten ist

und die mittlere Anzahl aller wartenden Anrufe
ist

Die Wahrscheinlichkeit P(>0) ist auch bei
sehr geringem Verkehr endlich. Je mehr sich das Angebot der Anzahl der Abnehmer
nähert, desto größer ist die mittlere Anzahl der wartenden Anrufe, während die
Wartewahrscheinlichkeit ebenso wie Pw(>r) sich dem Wert 1 nähert.
Wegen der negativ exponentiellen Verteilung
der Belegungsdauern besitzt auch die Wartezeit eine solche Verteilung. Ein
Anruf wartet also mit der Wahrscheinlichkeit

länger als die Zeit t auf den Beginn der
Bearbeitung. Dabei ist tw = tm/(n-A) die mittlere
Wartezeit der wartenden Anrufe. Auch bei sehr kleinem Angebot behält tw
mindestens den Wert tm/n, da, wenn ein Anruf überhaupt wartet er im
Mittel solange warten muß, bis einer der Abnehmer frei wird. Die mittlere
Wartezeit tw* aller Anrufe ist dagegen für kleine Werte des Angebots
ebenso wie die Wartewahrscheinlichkeit sehr klein.
Wahrscheinlichkeit
P(>t), daß die Wartezeit größer als die Zeit t ist, als Funktion der auf die
mittlere Belegungsdauer tm bezogene Zeit t bei einem auf die Anzahl
n der Abnehmer bezogenen Angebot A von 0.75 Erl, vollkommener Erreichbarkeit
und Zufallsverkehr 1.Art für verschiedene n
Beim eben betrachteten Beispiel war
vorausgesetzt worden, daß die Anrufe in der Reihenfolge des Eintreffens
abgefertigt werden ("first in, first out). Diese Voraussetzung beeinflußt die
Wahrscheinlichkeitsverteilung der Wartezeit. Die Wartewahrscheinlichkeit und
der Mittelwert der Wartezeit sind jedoch unabhängig von der
Warteschlangendisziplin, solange die zu erwartenden Belegungsdauern dabei nicht
berücksichtigt werden.
Der Einfluß der Warteschlangendisziplin zeigt
sich erst bei der Streuung der Wartezeiten.
Am häufigsten werden Warteschlangen nach der FIFO
(First In First Out) - Strategie, auch FCFS (First Come First
Serve) - Strategie genannt angelegt. Die ankommenden Anforderungen
werden in der Schlange hinten eingereiht und von vorne abgerufen. Die Strategie
wird als eine faire Strategie angesehen.
Die LIFO (Last In First Out) - Strategie,
auch LCFS (Last Come First Serve) - Strategie genannt, wird dann
angewandt, wenn die Bedeutung der Anforderungen mit der Zeit abnimmt. Die
zuletzt angekommene Anforderung wird deshalb als erste behandelt. Die
Warteschlange wird so angelegt, daß die ankommende Anforderung vorne eingereiht
wird und wiederum von vorne abgerufen wird.
In realen Systemen wird häufig eine
unterschiedliche Speicherkapazität für die Speicherung der einzelnen
Anforderungen erforderlich. Die Anforderungen werden in zufälliger Anordnung -
gerade wo der Speicherplatz ausreicht - abgelegt. Diese zufällige Strategie - Random
Queue genannt - hat keinen Einfluß auf die mittleren Wartezeiten.
Unabhängig von der Warteschlangendisziplin
sind die mittlere Anzahl und die mittlere Wartezeit der wartenden Anrufe. Die
Verteilung der Belegungsdauern ist nur soweit von Einfluß auf diese
Mittelwerte, wie sie zu unterschiedlichen Werten für die Streuung sm der Belegungsdauern führt:

Bei gleicher mittleren Belegungsdauer und gleichem
Angebot ist die mittlere Wartezeit am kleinsten bei konstanten Belegungsdauern
(sm = 0); bei negativ-exponentieller
Verteilung (sm = tm)
ist die Wartezeit doppelt so groß.
Mittlere Wartezeit
tw* aller Anrufe, bezogen auf die mittlere Belegungsdauer tm,
als Funktion des Angebots A bei negativ-exponentiell verteilten Anrufabständen
und einem Abnehmer für verschiedene Streuungen sm der Belegungsdauern
Wartesysteme
mit nichtunterbrechenden Prioritäten
Die Zuweisung von Prioritäten stellt eine
besondere Warteschlangendisziplin für den Gesamtvorgang dar, so daß die obigen
Beziehungen auch hier gelten, sofern bei Zuweisung von Prioritäten nicht nach
den zu erwartenden Belegungsdauern vorgegangen wird. Im folgenden wird speziell
vorrausgesetzt, daß die Belegungsdauern in den verschiedenen Prioritäten der
gleichen Verteilung genügen. Diese Vorraussetzung trifft für Systeme zu, bei
denen ein Abnehmer alle Anrufe, unabhängig von ihrer Priorität, in der gleichen
Weise verarbeitet, z.B. eine Speichervermittlung mit Teilnehmern, deren
Nachrichten bevorzugt abgefertigt werden, ohne daß diese sich im Aufbau des
Nachrichtenkopfes oder in der Nachrichtenlänge von den übrigen unterscheiden.
Außerdem sollen in jeder Priorität die Anrufe negativ-exponentiell verteilt
eintreffen.
Für den Anteil A1 am Gesamtangebot,
der mit höchster Priorität abgefertigt wird, ist nach wie vor die
Wartewahrscheinlichkeit genau so groß, wie für das Gesamtangebot, da bestehende
Belegungen nicht unterbrochen werden. Die Wartezeiten der wartenden Anrufe sind
aber kürzer, und zwar stimmt ihre Verteilung mit der Verteilung überein, die
sich ergibt, wenn überhaupt nur der Anteil A1 angeboten wird.
Die mittlere Wartezeit tw1 ist
entsprechend

gegenüber der mittleren Wartezeit tw
des Gesamtvorgangs verkürzt. Ahnliche Beziehungen gelten für die Anteile, die
mit niedrigeren Prioritäten abgefertigt werden. Bei geringem Gesamtverkehr ist
die Zuweisung von Prioritäten ohne große Auswirkung, bei hohem Verkehr wirken
sie sich dagegen sehr deutlich aus; vor allem bleiben die mittleren Wartezeiten
der wartenden Anrufe in allen Prioritäten außer der niedrigsten auch dann
endlich, wenn der Gesamtverkehr gegen n geht. Zur Erläuterung zeigt
untenstehendes Diagramm die mittlere Wartezeit aller Anrufe bei einer
gleichmäßigen Aufteilung in drei Prioritäten. Entsprechende Beziehungen gelten
auch für Systeme mit mehr als einem Abnehmer.
Mittlere
Wartezeiten tw* aller Anrufe bzw. aller Anrufe mit einer von drei
Prioritäten tw1* bis tw3* bei negativ-exponentiell
verteilten Anrufabständen, gleichmäßiger Aufteilung des Angebotes auf die
Prioritäten und einem Abnehmer
Weitere
Systeme mit Wartemöglichkeit
Die in den bisherigen Betrachtungen getroffene
Annahme, daß die Warteschlangen unbegrenzt sind, d.h. mindestens so viele
Plätze enthalten, wie es Zubringer gibt, ist nicht immer erfüllt. In einem
System mit begrenzter Wartemöglichkeit ist die Verlustwahrscheinlichkeit
geringer als bei einem reinen Verlustsystem, die mittlere Wartezeit geringer
als bei einem Wartesystem ohne Begrenzung.
Kommt es in einem System darauf an, nicht nur
die mittlere Wartezeit der wartenden Anrufe mit höheren Prioritäten zu
verringern, sondern auch die Wartewahrscheinlichkeit, so müssen Belegungen
niederer Priorität unterbrechbar sein. Der Verkehr mit höchster Priorität wird
dann so abgefertigt, als gäbe es nur diesen Anteil. Die Wartewahrscheinlichkeit
sinkt entsprechend, und die Warteverteilung wird innerhalb dieser Priorität nur
durch die Belegungsdauern dieser Priorität selbst bestimmt.
Durch eine andere Maßnahme kann die mittlere
Wartezeit aller Rufe minimiert werden und zwar dadurch, daß Anrufe mit der
kürzesten zu erwartenden Belegungsdauer mit höchster Priorität abgefertigt
werden.
Verkehrsmessungen
Messungen
von Parametern
In den vorhergehenden Abschnitten wurden
verkehrstheoretische Fragen an Hand bestimmter Verteilungen erörtert. Kann man
in dieser Weise den Funktionsverlauf voraussetzen, also z.B. sagen, daß eine
negativ-exponentielle Verteilung vorliegt, dann besteht die Aufgabe von
Verkehrsmessungen darin, die Parameter der Verteilung zu ermitteln, etwa den mittleren
Anrufabstand und zwar für die Hauptverkehrsstunde, die selbst
ebenfalls durch Messungen bestimmt werden muß. Dabei kann sich für manche
Datennetze ergeben, daß es keine ausgeprägte Konzentration des Verkehrs auf
einen solchen Zeitraum gibt.
Die Messung der Parameter ist vor allem
erforderlich, um langfristige Anderungen im Verkehr feststellen zu können,
damit die Vermittlungseinrichtungen rechtzeitig den veränderten Anforderungen
angepaßt werden können. Von solchen langfristigen Anderungen sind kurzfristige
zu unterscheiden, wie sie sich z.B. bei Übergängen von verkehrsschwachen zu
verkehrsstarken Zeiten oder umgekehrt zeigen.
Ermittlung
von Verteilungsfunktionen
In der Regel kann man aber nicht davon
ausgehen, daß die Verteilungen in ihrem Funktionsverlauf bekannt sind. Es wäre
also wünschenswert, auch die Verteilung selbst aus den Meßgrößen ableiten zu
können. Praktisch begnügt man sich mit der annähernden Ermittlung einiger
Momente. Davon ausgehend kann man eine unbekannte Verteilung durch eine andere
beschreiben, die mit ihr in den Momenten übereinstimmt.
Umfang
der Messungen
Ein besonderes Problem entsteht bei
unbekannten Verteilungen hinsichtlich des Umfangs der Messungen, die
erforderlich sind, um die Parameter genügend genau zu bestimmen. Unter
Genauigkeit ist hier ein Paar von Begriffen zu verstehen, nämlich das Vertrauensintervall
I und die statistische Sicherheit S. Das Vertrauensintervall gibt an,
wie weit der wahre Wert von dem aus Messungen gewonnenen Wert abweichen kann.
Die statistische Sicherheit gibt an, mit welcher Wahrscheinlichkeit das
Vertrauensintervall zutrifft. Auf Grund eines bestimmten Umfangs der Meßwerte
kann man ein enges Vertrauensintervall mit geringer oder ein breiteres
Vertrauensintervall mit höherer statistischer Sicherheit behaupten.
Vertrauensintervall
I als Funktion der Anzahl n der Messungen bei Zufallsverkehr 1.Art für
verschiedene Werte der statistischen Sicherheit S
Für Verteilungen der Belegungsdauer mit
größerer Streuung sind mehr, für Verteilungen mit geringerer Streuung weniger
Messungen erforderlich, um zum gleichen Vertrauensintervall bei gleicher
statistischer Sicherheit zu kommen.
Durchführung
der Messungen
Eine einfache Möglichkeit zur Messung von
Parametern besteht darin, fortlaufend den Belegungszustand der betreffenden
Einrichtung zu messen und daraus die im einzelnen interessierenden Größen zu
ermitteln. Voraussetzung dafür ist, daß es eine der Messung zugängliche
Darstellung des Belegungszustandes gibt, sei es eine mit der Belegung gegebene
physikalische Größe, die dann durch spezielle Meßgeräte erfaßt wird, sei es ein
Abbild des Belegungszustandes, z.B. im Speicher einer Vermittlungsstelle mit
speicherprogrammierter Steuerung, daß durch ein Meßprogramm bearbeitet werden
kann.
Genauere Angaben über den Verkehr lassen sich
dadurch gewinnen, daß Angaben über die einzelnen Belegungen aufgezeichnet
werden. Bei zentralgesteuerten Vermittlungsstellen ist eine vollständige
Aufzeichnung aller Rufdaten möglich (Zeitpunkt und Inhalt aller Steuersignale
vom Ruf bis zur Schlußzeichenbestätigung) und durch Verarbeitung dieser Daten
eine genaue Analyse des gesamten Verkehrs.
Weitere
Anwendungen der Verkehrstheorie
Die Verkehrstheorie beschäftigt sich neben der
Wahrscheinlichkeitsrechnung für Warte- und Verlustsysteme auch mit
Koppelanordnungen; d.h. wie diese dimensioniert werden, damit jeder Teilnehmer
mit jedem telefonieren kann, ohne daß Unmengen an Koppelpunkten verwendet
werden.
Eine Koppelmatrix (siehe Punkt 1.3.) hätte zum
Beispiel den Vorteil, daß stets, wenn ein Teilnehmer A (an der i-Seite) eine
Verbindung mit einem Teilnehmer B (an der k-Seite) wünscht und der Teilnehmer B
frei ist, die Verbindung auch durchgeschaltet werden kann. Man nennt eine
Koppelanordnung mit dieser Eigenschaft blockierungsfrei. Verzichtet man auf
diese Blockierungsfreiheit, so kommt man mit wesentlich weniger Koppelpunkten
aus. Dies ist besonders wichtig bei einer großen Anzahl von Teilnehmern, denn
die Anzahl der Koppelpunkte wächst in diesem Beispiel quadratisch mit der
Teilnehmerzahl. Deshalb versucht man mit Hilfe der Verkehrstheorie die
Koppelpunkte in den Koppelanordnungen möglichst günstig einzusetzen, um für
möglichst viele Teilnehmer möglichst wenig Koppelpunkte zu verwenden.
Quellenangaben
P. Bocker: Datenübertragung / Band I. -
Grundlagen
Gerd Siegmund: Technick der Netze
Firoz Kaderali: Digitale Kommunikationstechnik
II.
Diverse Schülerreferate








 ,
,
